Bis jetzt habe ich noch nichts zu E = mc2 gesagt. Und ich habe auch nicht vor, diesbezüglich tiefer einzusteigen. Man kann die Massenformel der Relativitätstheorie auch mit Minkowski-Diagrammen ableiten, aber es erfordert an einer Stelle einen "leap of faith", den ich den Lesern nicht zumuten möchte.
Zudem kann man aus der Massenformel *nicht* schließen, dass Überlichtgeschwindigkeiten unmöglich seien. Nimmt man etwa an, dass es Teilchen mit *imaginärer* Ruhmasse gibt (das sind die Tachyonen), dann *müssen* die sogar schneller als das Licht sein, um eine reelle Energie zu haben.
Allerdings hätte ihre Existenz eigenartige Konsequenzen, wenn das Bild der Raumzeit, das uns die spezielle Relativitätstheorie nahelegt, richtig ist. Das soll anhand einer kleinen Science-fiction-Geschichte illustriert werden.
Wir setzen voraus, dass Tachyonen in neuartigen Waffen als tödlicher Energiestrahl benützt werden können. Diese Waffen sind gerade vor Stellas Flug zum Alpha Centauri erfunden worden. Alf und Bert sind zwei junge Männer, die um Stellas Gunst bemüht sind. Nur einer kann aber mit nach Alpha Centauri. Deshalb beschließen sie, sich zu duellieren.
Das
Duell geht so: sie fliegen mit Raumscootern, das sind die kleinen Raketen
im Bild, 10 Sekunden lang auseinander. Dann drehen sich beide um und schießen
mit ihren Tachyonenpistolen aufeinander.
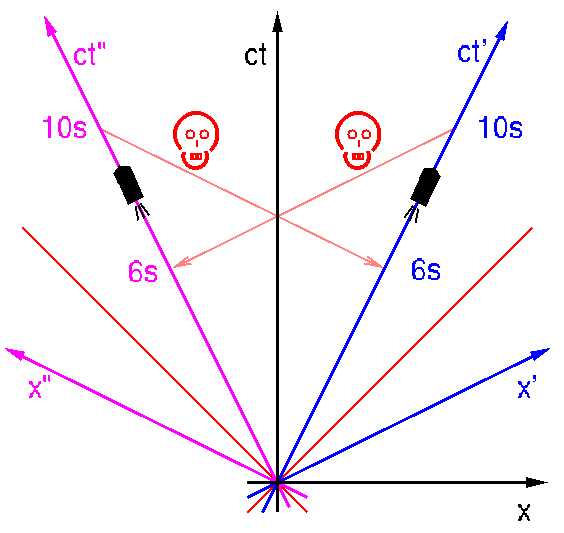
Die Raumflüge verlaufen im Rahmen der normalen Physik. Die Relativgeschwindigkeit der beiden sei (+-)4/5 c, dann ist der Zeitdilatationsfaktor 3/5. Die Tachyonen sollen so schnell sein, dass sie sich praktisch in Nullzeit ausbreiten, d.h. im Diagramm fliegen sie nahezu parallel zur Achse x' bzw. x" (die ja gleichzeitige Ereignisse verbinden). Dass die beiden Raumschiffe langsamer als das Licht sind, sieht man daran, dass die Steigungen ihrer Weltlinien (betragsmäßig) größer als die des Lichtkegels sind. Die Tachyonen sind schneller als das Licht und ihre Weltlinien haben eine betragsmäßig kleinere Steigung als die des Lichts.
Unsere Helden drehen sich also jeweils nach 10 Sekunden um und ballern los. Alf, dessen Weltlinie blau ist, trifft gut. Bert wird also von Alfs Strahl getötet, und nach Alfs Rechnung sind auf Berts Uhr erst 6 Sekunden vergangen. Bert rechnet aber anders. Da für ihn Alfs Zeit langsamer geht, hat Alf noch nicht geschossen, wenn seine 10 Sekunden um sind. Und Bert schießt auch gut. Er tötet also Alf zu einem Zeitpunkt, wo auf dessen Uhr 6 Sekunden um sind. Dann kommt Alf aber gar nicht mehr dazu, ihn zu erschießen. Das gleiche Argument gilt aber auch für Bert. Da Alf auf ihn schießen kann, bevor seine 10 Sekunden um sind (nach Alfs Uhr), wird er schon nach 6 Sekunden tödlich getroffen und kommt nicht mehr dazu, Alf zu erschießen. Da er aber Alf nach 6 Sekunden (auf dessen Uhr) trifft, kann dieser ihn nicht mehr erschießen. Und so weiter, ad infinitum.
Ein echtes Paradox. Und wir sehen auch, dass im schwarzen Koordinatensystem (dem des Schiedsrichters) die Tachyonenstrahlen in die Vergangenheit gehen. Es handelt sich also um ein Zeitparadox mit entsprechender Kausalitätsverletzung. Jeder erschießt den anderen, bevor der ihn töten kann. Da dann aber jeder getötet wird, bevor er schießen kann, erschießt keiner den anderen, bevor die Waffen benützt werden. Dann aber kann wieder geschossen werden, und man tötet sich...
Es gibt verschiedene Möglichkeiten, diesen Konsequenzen auszuweichen. Die einfachste, allgemein anerkannte, ist, überlichtschnelle Signale und damit Tachyonen auszuschließen. Warum ist das notwendig und hinreichend? Ein überlichtschnelles Signal hat eine Trajektorie, die "flacher" ist als der Lichtkegel. Es kann also ein Bezugssystem gefunden werden, in dem seine Weltlinie die x'-Achse eines sich unterlichtschnell bewegenden Beobachters ist. In diesem Bezugssystem bewegt sich das Signal unendlich schnell. Für einen Beobachter, der noch ein bisschen schneller fliegt, geht es sogar in die Vergangenheit, womit prinzipiell eine Situation wie die eben für Alf und Bert geschilderte möglich wird (dazu sind also nicht *extrem* schnelle Tachyonen nötig -- es reicht, wenn sie nur wenig schneller sind als das Licht). Wenn aber alle Signale unterlichtschnell sind, kann keines parallel zur x'-Achse eines Beobachters laufen, weil diese Achsen für unterlichtschnell bewegte Beobachter alle flacher verlaufen als der Lichtkegel. Damit ist ein Paradoxon wie das geschilderte ausgeschlossen. Man kann zeigen, dass ein unterlichtschnelles Signal in *allen* Bezugssystemen unterlichtschnell ist.
*Das* ist also der Grund, warum die spezielle Relativitätstheorie überlichtschnelle Signale (und damit auch Reisen) ausschließt (wenn das Kausalprinzip gilt -- dazu später mehr). Es ist nicht so wichtig, dass bei Annäherung an die Lichtgeschwindigkeit Massen unendlich groß werden (das könnte man ja umgehen, indem man die "Lichtbarriere durchtunnelt", also nie exakt mit Lichtgeschwindigkeit fliegt). Aber,und das ist der springende Punkt, wenn die von der Relativitätstheorie behauptete Struktur der Raumzeit richtig ist, dann ist es völlig unabhängig davon, auf *welche Weise* man Überlichtgeschwindigkeit erreicht. Man kann sie für das Senden von Signalen in die Vergangenheit verwenden und damit Paradoxa produzieren.
Welche anderen Möglichkeiten gibt es, dem Paradoxon auszuweichen? Immerhin sind in der Physik Tachyonen ja ernsthaft in Erwägung gezogen worden. Eine Lösung wäre, dass man bei diesen Teilchen nicht zwischen Emission und Absorption unterscheiden könnte. Dann ließen sich die Tachyonenstrahlen von Alf und Bert uminterpretieren: die pinken Pfeile müssten aus der Sicht des schwarzen Beobachters in ihrer Richtung umgedreht werden und würden nun in die Zukunft gehen. Allerdings wäre eine Pistole, bei der man nicht entscheiden kann, ob sie schießt oder gerade einen Treffer kassiert, nicht sehr nützlich... Außerdem hätten die Tachyonen dann je nach Bezugssystem auch mal negative Energien, was andere unangenehme Konsequenzen hätte... Man könnte auch (motiviert durch Erfahrungen mit der Quantenmechanik) daran denken, dass Tachyonen nur bedingt kontrollierbar sind. Doch das genügt nur dann zur Vermeidung des Paradoxons, wenn die bedingten Kontrollen der beiden Strahlen *korreliert* sind. Denn bei *unabhängigen* Ergebnissen der Schießversuche würde, auch wenn jeder der beiden Schützen nur mit einprozentiger Wahrscheinlichkeit einen Tachyonenstrahl zustandebringt (was die Nutzung als Waffe de facto ausschlösse), doch mit einer Wahrscheinlichkeit von 1/10000 ein Paradoxon zustandekommen. Was es braucht, ist die Verhinderung eines Treffers aufgrund der Tatsache, dass die beiden Tachyonenstrahlen einander begegnen! Man ist schon geneigt, Korrelationen dieser Art ins Reich der Magie zu verweisen.
Ferner ließe sich das Paradoxon auch vermeiden, wenn man die Willens- oder besser Handlungsfreiheit der Protagonisten verneint. Wenn sie nicht frei sind zu schießen, kann immer einer irgendwie daran gehindert sein oder danebenschießen (was heißt kann: muss). Welche Gesetze aber dies regeln sollen, bleibt schleierhaft...
Einen etwas befriedigenderen Weg, der aber auf eine Abschaffung der speziellen Relativitätstheorie hinausläuft, werde ich im letzten Abschnitt des Kurses besprechen.
Next: Auflösung Bellsches Paradoxon Up:Spezielle Relativitätstheorie Previous: Zwillingsparadoxon
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO