Hier kommt die versprochene Auflösung des Bellschen Raumschiffparadoxons. Wenn man die Lorentz-Kontraktion als "real" ansieht, ist die Sache eigentlich klar: ein nicht auf Zug beanspruchtes Seil wird sich verkürzen, wenn es in Bewegung gesetzt wird. Die Gleichgewichtslänge des Seils ist also geringer als im Ruhezustand. Hält man es durch die beiden Raumschiffe auf einer festen Länge (s. Bild), so wird es unter Zugspannung stehen und wenn diese zu groß wird, muss es schließlich reißen.

Insbesondere bedeutet das, dass das *Hookesche Gesetz* im Rahmen der Relativitätstheorie zu modifizieren ist. Denn es besagt ja, dass elastische Spannungen nur auftreten, wenn man das Objekt deformiert. Hier aber bleibt das Seil gleich lang, und es treten trotzdem Spannungen auf. Die Modifikation des Hookeschen Gesetzes, die nötig ist, um es relativistisch invariant zu machen, hat schon kurz nach der Einführung der speziellen Relativitätstheorie ein gewisser Herr Gron vorgestellt. (Der hat auch noch andere schöne Sachen gemacht, etwa beschrieben, wie die Welt auf einer rotierenden Scheibe aussieht.)
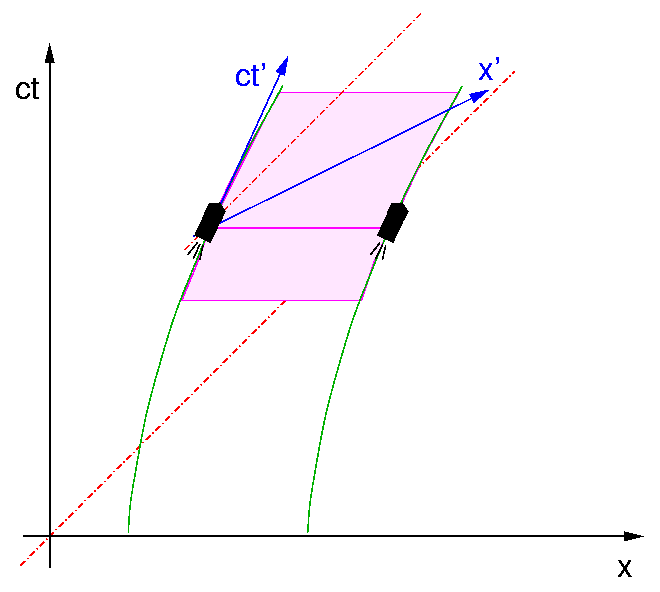
Die Frage, ob und warum das Seil reißt, sollte sich aber auch aus der Perspektive des Seils vernünftig beantworten lassen. Schauen wir uns deshalb das Bild noch ein wenig genauer an. Grün sind die Weltlinien der beiden Raumschiffe gezeichnet. Die beiden Raumschiffbildchen und die magentafarbene Linie geben die Positionen der Raumschiffe und des Seils zu einem herausgegriffenen Zeitpunkt an, wie sie der Inertialbeobachter beschreiben würde, der im schwarzen Koordinatensystem lebt.
Für das Seil gibt es, da es sich um ein ausgedehntes beschleunigtes Objekt handelt, gar kein *einzelnes* Bezugssystem. Jeder Punkt des Seils hat sein eigenes Bezugssystem. Gleichzeitigkeit für ein beschleunigtes System festzulegen, ist keine triviale Aufgabe. Die naheliegendste Lösung besteht darin, zu sagen, dass für den beschleunigten Punkt als gleichzeitig gilt, was für einen sich am selben Ort befindenden Beobachter gleichzeitig ist, der sich mit einer konstanten Geschwindigkeit bewegt, die mit der *momentanen* Geschwindigkeit des Punktes übereinstimmt. Betrachten wir der Einfachheit halber den hinteren Befestigungspunkt des Seils. Die Zeitachse (ct') für diesen Punkt ist die Tangente an seine Weltlinie, die Raumachse (x'), welche Gleichzeitigkeit festlegt, erhält man durch Spiegelung an einer lokalen Lichtweltlinie (die ja die Winkelhalbierende der Zeit- und Raumachse sein muss). Die magentafarbene Fläche ist die "Weltfläche" des ausgedehnten Objekts Seil. Und nun ist es offenbar, dass für den hinteren Endpunkt des Seils der *vordere* Endpunkt sich dort befindet, wo die x'-Achse die Weltlinie des Seilvorderendes schneidet (rechte grüne Kurve). Das Seil liegt also entlang der x'-Achse. Wir können auch ohne Konstruktion von Maßstabshyperbeln sehen, dass das eine *Verlängerung* des Seils bedeutet. Denn die *Geschwindigkeit* des vorderen Raumschiffs (und damit auch des Seilvorderendes) ist am Schnittpunkt der x'-Achse mit seiner Weltlinie *größer* als die des hinteren am Schnittpunkt der x'-Achse mit dessen Weltlinie. (Die Weltlinie am vorderen Schnittpunkt ist flacher als die am hinteren.) Das heißt aber, dass vom hinteren Raumschiff aus gesehen die Entfernung des vorderen immer weiter anwächst, der Abstand der beiden Raumschiffe ist eben *nicht* konstant, sondern *nimmt zu*. Damit wird das Seil gespannt und muss schließlich reißen.
Nachdem wir nun das Bellsche "Paradoxon" zu aller Zufriedenheit gelöst haben, wollen wir uns mit den Implikationen von Tachyonenpistolen und anderen Mitteln der Überschreitung der Lichtgeschwindigkeit befassen. Wir werden sehen, dass das zu tun hat mit der Frage der Kausalität.
Next: Kausalität Up:Spezielle Relativitätstheorie Previous: Tachyonenpistolenduell
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO