3.2 Maßstäbe

Next: Zeitdilatation   Up: Spezielle Relativitätstheorie   Previous: Lorentz-Transformationen

Im Abschnitt über die Newtonsche Physik hatte ich gesagt, dass man bei schiefwinkligen Koordinatensystemen immer ein bisschen achtgeben muss, wie Maßstäbe definiert sind. Im Fall der Galilei-Transformation erhielten wir den Zeitmaßstab unter Ausnützung der Absolutheit der Newtonschen Zeit. Der Raummaßstab war für beide Beobachter derselbe.

Im Fall der Lorentz-Transformationen muss man anders vorgehen. Was man braucht, um Maßstäbe festlegen zu können, ist eine Kurve (Hyperfläche), die in beiden Koordinatensystemen dieselbe ist; der technische Ausdruck ist, dass sie *invariant* unter der Koordinatentransformation ist.

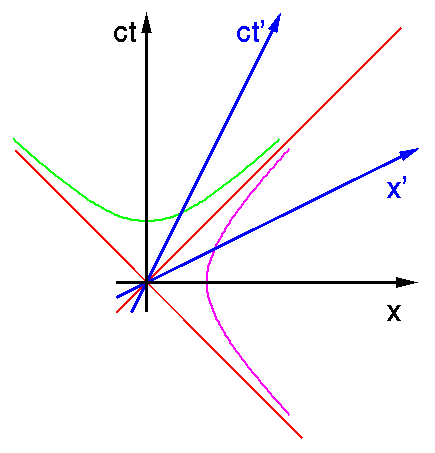
Einen Typ solcher Kurven kennen wir bereits: die Weltlinien von Licht, im nebenstehenden Bild rot gezeichnet. Sie sehen für beide Beobachter exakt gleich aus. Diese Weltlinien nennt man *Lichtkegel* und zwar den Teil oberhalb der "Gegenwart" Vorwärtslichtkegel, den in der Vergangenheit liegenden Rückwärtslichtkegel.

Zur Maßstabsfestlegung kann man andere invariante Kurven verwenden, nämlich Hyperbeln, deren Asymptoten gerade auf dem Lichtkegel liegen. Wie man *ohne Mathematik* zeigen kann, dass solche Kurven invariant sind, weiß ich nicht. Wenn jemand eine gute Idee hat -- ich bin interessiert. *Dass* diese Hyperbeln invariant sind, setzen wir hier also ohne Beweis voraus.

Was ihre Invarianz bedeutet, ist dann wieder einfach. Die grüne Hyperbel, die die Zeitachsen schneidet, tut das für beide Beobachter im selben Abstand. Die Zeitintervalle von t=0 zum Schnittpunkt der Hyperbel mitder ct-Achse und von t'=0 zu ihrem Schnittpunkt mit der ct'-Achse sind also gleich lang! Damit können wir einen Zeitmaßstab einführen. Wir legen ein Zeitintervall von 1 Sekunde im (xt)-System fest und konstruieren die Hyperbel, die bei t=1 Sek. die ct-Achse senkrecht schneidet und deren Asymptoten durch den Lichtkegel gegeben sind. Dann ist der Schnittpunkt mit der ct'-Achse bei t' = 1 Sekunde.

Völlig analog verfährt man mit Längen. Schneidet die magentafarbene Hyperbel die x-Achse bei x = 1 m, so ist ihr Schnittpunkt mit der x'-Achse bei x' = 1 m.

Mit diesem Wissen ausgerüstet, können wir mehr als die bloße Gleichzeitigkeit diskutieren (dafür reichte die Parallelprojektion). Wir können gemessene Zeit- und Längenintervalle in den beiden Systemen *vergleichen*.

Next: Zeitdilatation   Up: Spezielle Relativitätstheorie   Previous: Lorentz-Transformationen

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO