3.3 Die Zeitdilatation

Nehmen wir mal an, der schwarze und blaue Beobachter haben, als sie sich trafen (das ist das Ereignis "Koordinatenursprung des gezeigten Bildes"), ihre Uhren auf dieselbe Zeit gestellt, um konkret zu sein, auf 12:00 Uhr.

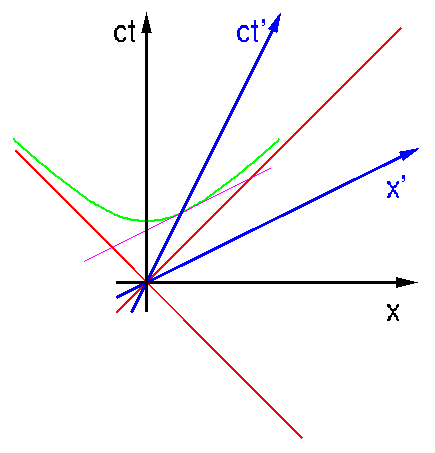
Eine Stunde später, also um 1:00 Uhr auf seiner Uhr, will der blaue Beobachter wissen, wie spät es gerade bei dem schwarzen ist. Um das rauszukriegen, muss er bloß feststellen, wann die Parallele zu seiner x'-Achse (eine Linie gleicher Zeiten) die ct-Achse schneidet. Offensichtlich tut sie das zu einer Zeit, die *vor* dem Schnittpunkt der grünen Maßstabshyperbel mit der ct-Achse liegt. (Die Parallele ist Tangente an die Hyperbel.)

Also schließt der blaue Beobachter, dass um 1:00 Uhr bei dem schwarzen noch nicht 1:00 Uhr ist; das heißt, die Zeit des schwarzen Beobachters läuft langsamer. Sie dehnt sich gewissermaßen, um das kürzere Intervall auf das längere (von 1 Stunde Dauer) auszudehnen, daher der Name *Zeitdilatation*.

Nun wollen wir uns anschauen, wie die Dinge aus der Sicht des schwarzen Beobachters liegen; dazu werfen wir einen Blick auf Bild rechts. Er schaut um 1:00 Uhr auf seine Uhr und überlegt sich, wie spät es jetzt wohl bei dem blauen Beobachter ist. Nichts leichter als das: waagerechte Tangente an die Maßstabshyperbel, was zeigt, dass es bei dem blauen Beobachter noch nicht 1:00 Uhr ist. Also geht die Zeit des blauen langsamer. Na ja, nichts besonderes; das ist eben die Zeitdilatation.

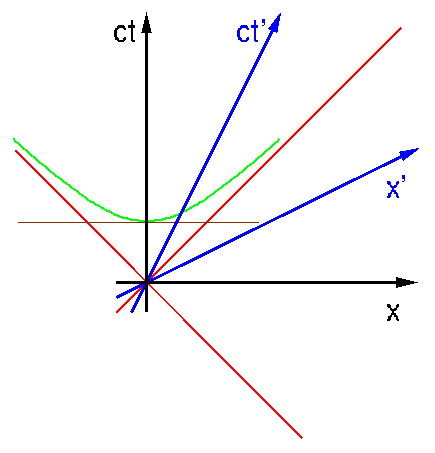Hoppla, kann das denn stimmen? Jeder der beiden Beobachter stellt fest, dass die Zeit des anderen langsamer geht. Nach dem Relativitätsprinzip kann es nicht anders sein, denn sonst könnte man *ein* Bezugssystem auszeichnen und "ruhend" nennen -- es wäre das, in dem die Zeit am schnellsten geht. Andererseits widerspricht die Idee, dass, wenn die Zeit des anderen aus meiner Sicht langsamer geht, meine eigene Zeit aus dessen Sicht *nicht* schneller geht, sondern *auch* langsamer, doch sehr der Intuition.

Aber ein echter Widerspruch entsteht natürlich nicht. Dass jeder feststellen kann,  die Zeit des anderen gehe langsamer als die eigene, liegt natürlich daran, dass die Gleichzeitigkeiten der beiden verschieden festgelegt sind. Gäbe es eine absolute Gleichzeitigkeit, wäre eine solche Folgerung in sich widersprüchlich. Es kann nicht, wenn es bei dem einen 1:00 Uhr ist, beim anderen gleichzeitig vor *und* nach 1:00 Uhr sein. Aber es kann sehr wohl mit der Gleichzeitigkeit des schwarzen Beobachters *nach* 1:00 Uhr sein, wenn es auf der Uhr des blauen genau 1:00 Uhr ist (zweites Bild ), *und* mit der Gleichzeitigkeit des blauen Beobachters vor 1:00 Uhr beim schwarzen, wenn es bei ihm 1:00 Uhr ist (erstes Bild). Die Absolutheit der Zeit ist eben aufgehoben.

Next: Längenkontraktion   Up: Spezielle Relativitätstheorie   Previous: Maßstäbe

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO