3.1 Die Lorentz-Transformationen

Next: Maßstäbe   Up: Spezielle Relativitätstheorie   Previous: Spezielle Relativitätstheorie
 

Wie lässt sich das vereinbaren? Nun, es muss eben so sein, dass die Galilei-Transformationen nicht die richtigen Transformationen sind, wenn man vom Bezugssystem eines Beobachters in das eines relativ dazu mit konstanter Geschwindigkeit bewegten anderen Beobachters umrechnen will.

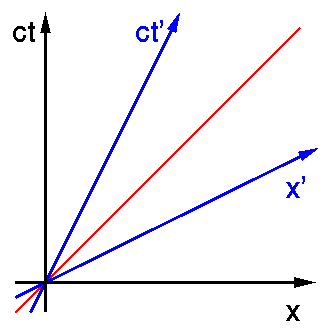Wie die richtigen Transformationen wirken müssen, kann man sich anhand eines Bildes klarmachen. Hier habe ich statt t an die Zeitachse ct geschrieben. Das hat den Vorteil, dass ein vom Ursprung nach rechts gehender Lichtstrahl sich in diesem Koordinatensystem entlang der ersten Winkelhalbierenden bewegt (rote Linie), denn die in der Zeit t zurückgelegte Strecke ist natürlich x=ct. (Die Zeit wird also in Metern vom Licht zurückgelegter Strecke gemessen.)

Nun wollen wir das Koordinatensystem eines sich relativ zum (xt)-System mit konstanter Geschwindigkeit bewegenden Beobachters konstruieren. An der ct'-Achse können wir nicht rütteln, die ist zwangsläufig durch die Weltlinie des Beobachters (also seine Geschwindigkeit) festgelegt. Aber dann sagt uns unser zweites Postulat, dass das Licht sich mit der Geschwindigkeit c bewegen muss. Das heißt, die rote Weltlinie des Lichts muss auch für unser (x' t')-System erste Winkelhalbierende sein. Wäre es nicht so, hätte das Licht ja eine andere Geschwindigkeit als c im (x' t')-System. Jetzt ist also die x'-Achse nicht mehr mit der x-Achse identisch. Was bedeutet das? Da die Raumachsen Orte gleichzeiter Ereignisse sind (denn die x-Achse ist durch ct=0 gegeben, die x'-Achse durch ct'=0), sind an verschiedenen Orten stattfindende Ereignisse, die für den Beobachter im schwarzen Koordinatensystem gleichzeitig stattfinden, *nicht* gleichzeitig für den im blauen Koordinatensystem ruhenden Beobachter und umgekehrt.

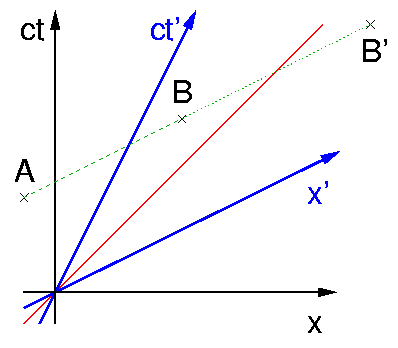
Das ist sicher etwas gewöhnungsbedürftig und soll deshalb nochmal explizit mit einem Bild demonstriert werden. A und B sind zwei Ereignisse, die im blauen System gleichzeitig sind -- ihre Verbindungslinie ist eine zur x'-Achse parallele Gerade. Im schwarzen System findet B *nach* A statt.

Zwei Dinge sollte man sich noch klarmachen. Führt man den Punkt B näher an A heran, bis sie zusammenfallen, so stimmen beide Beobachter bezüglich der Gleichzeitigkeit der Ereignisse A und B überein. Eine "Meinungsverschiedenheit" ist also nur möglich, wenn A und B räumlich getrennte Ereignisse sind. Wenn man andererseits B entlang der Parallelen zur x'-Achse weiter von A entfernt, etwa bis zum Punkt B', dann sind A und B' für den blauen Beobachter immer noch gleichzeitig, aber für den schwarzen ist ihr zeitlicher Abstand größer geworden -- B' liegt noch später als B.

Zweifellos seltsame Schlussfolgerungen. Aber sie können nicht einfach deshalb von der Hand gewiesen werden, weil unsere Alltagserfahrungen nicht damit zusammenzupassen scheinen. Denn die Alltagsvorstellung, dass Gleichzeitigkeit etwas Absolutes sei, ist ja leicht zu erklären: alle im Alltag vorkommenden Relativgeschwindigkeiten sind so klein gegenüber der Lichtgeschwindigkeit, dass die Neigung der x'-Achse gar nicht auffällt und Interpretationen im Rahmen der Galilei-Transformationen quantitativ richtig bleiben. Wenn man aber große Geschwindigkeiten hat (d.h. der Winkel zwischen ct- und ct'-Achse groß ist) oder aber große Entfernungen, dann macht sich der Unterschied zwischen den Galilei-Transformationen und den richtigen Transformationen, den *Lorentz-Transformationen*, durchaus bemerkbar.

Dass unsere bisherigen Schlussfolgerungen *unlogisch* wären, ist jedenfalls eine nicht haltbare Aussage. Sie sind zwangsläufige Konsequenzen der beiden Ausgangspostulate. Wenn sie falsch sind, muss eines der Postulate falsch sein. Ziehen wir an dieser Stelle eine kurze Zwischenbilanz: Aus der Gültigkeit des Relativitätsprinzips plus der Konstanz der Vakuumlichtgeschwindigkeit folgt, dass Gleichzeitigkeit keine absolute Bedeutung hat, sondern beobachterabhängig ist. Man sollte noch hinzufügen, dass -- im Rahmen der *speziellen* Relativitätstheorie -- die Gleichzeitigkeit eines Beobachters mit *gegebenem* Bewegungszustand durchaus *objektiv* ist. Das heißt, der "schwarze" Beobachter kann feststellen, dass die Ereignisse A und B im oben gezeigten Bild für den "blauen" Beobachter gleichzeitig sein müssen (auch wenn sie es für ihn selbst nicht sind). Es besteht also keine subjektive Beliebigkeit.

Noch eine Anmerkung: die Raum-Zeit-Diagramme zur Veranschaulichung der Lorentz-Transformationen nennt man *Minkowski-Diagramme*.

Next: Maßstäbe   Up: Spezielle Relativitätstheorie   Previous: Spezielle Relativitätstheorie

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO