Das Stab-Scheune-Paradoxon
Next: Up: Einleitung
spezielle Relativitätstheorie
Ein scheinbares Paradoxon zur Längenkontraktion begegnet dem Relativitätsinteressierten zum Beispiel beim Stab-Scheune-Gedankenexperiment. In der Literatur findet man es in verschiedenen Versionen (ein Auto in einer Garage, ein Zug in einem Tunnel...), das Grundproblem, welches hinter allen Varianten steckt, ist jedoch das gleiche. In unserem Fall sieht es wie folgt aus: Ein Stab bewegt sich mit gleichförmiger Geschwindigkeit in eine Scheune.
In Ruhe haben der Stab und die Scheune die gleiche Länge, QP = FR (s. Abb.).
Man nimmt an, der sehr athletische Läufer trägt den Stab mit hinreichend großer Geschwindigkeit gleichförmig durch die Scheune.
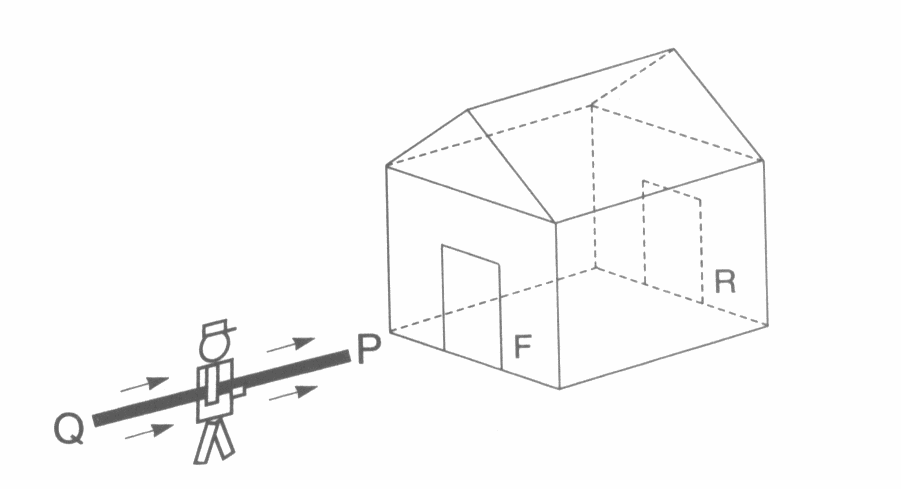
Es stellt sich nun die Frage: Passt der Stab in das Gebäude?
Gemäß der Längen- oder Lorentzkontraktion ist, von einem ruhenden Bezugssystem aus gesehen, ein bewegter Körper verkürzt.
Das bedeutet:
1) Aus der Sicht der Scheune besitzt der Stab eine Geschwindigkeit v und ist deshalb verkürzt, er passt also in die Scheune.
2) Aus der Sicht des Stabs bewegt
sich jedoch die Scheune mit der Geschwindigkeit
-v auf ihn zu, die Scheune ist verkürzt und der Stab
passt
nicht hinein.
Welcher Fall tritt ein, bzw. welche
Beschreibung ist richtig?
Zur Klärung des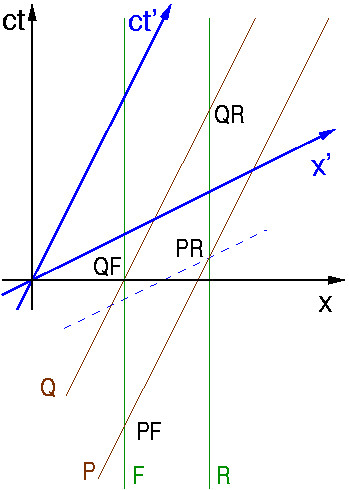
Problems ist ein Raum-Zeit-Diagramm
hilfreich. (Siehe die Erläuterung von Minkowski-Diagrammen im
Abschnitt Die
Lorentz-Transformation). Hier stellt
das Koordinatensystem
x,ct das Bezugssystem der Scheune dar und das Koordinatensystem x',ct'
das des Stabes.
Zur Klärung des
Problems ist ein Raum-Zeit-Diagramm
hilfreich. (Siehe die Erläuterung von Minkowski-Diagrammen im
Abschnitt Die
Lorentz-Transformation). Hier stellt
das Koordinatensystem
x,ct das Bezugssystem der Scheune dar und das Koordinatensystem x',ct'
das des Stabes.Die Geraden F und R
sind die Weltlinien des Vorderendes
(Eingangstür) und des Hinterendes (Ausgangstür) der Scheune,
die Geraden P und Q die Weltlinien des Vorderendes und Hinterendes des
Stabs. Es gibt 4 Schnittpunkte der Geraden, die das Passieren des Stabs
durch das Gebäude kennzeichnen.
Betrachten wir
zunächst die Scheune als ruhend und den Stab als bewegt, sprich
wir begeben uns in das x,ct-System. Da die Zeitachse die Ordinate ist,
tritt das Ereignis PF (das Eindringen des Stabs in die Scheune) als
erstes auf.
Gleichzeitige Ereignisse liegen immer auf Parallelen zur Abszisse, es
folgt also der Punkt QF (das Ende des Stabs passiert die
Vordertür) und erst dann PR, also der Durchgang der
Stabvorderseite durch die
Ausgangstür. (QR beschreibt dementsprechend das Ereignis "das
Stabende verlässt die Hintertür").
Der Stab hat also komplett in die Scheune gepasst.
Nun betrachten wir die Situation aus der Sicht des Stabs, also aus dem x',ct'-System. PF geschieht auch hier wieder als erstes. Mit Hilfe einer Parallelen zur x'-Achse (die gestrichelte blaue Linie) wird jedoch deutlich, dass das Austreten des Stabendes P aus der Tür R vor dem Eintreten des Stabendes Q in die Tür F liegt. Das heißt, das vordere Stabende verlässt die Scheune (PR) und erst dann passiert das Ende des Stabes die Eingangstür (QF), der Stab war demnach nie vollständig in der Scheune.
Es mag paradox klingen, dennoch sind beide Darstellungen richtig. Es handelt sich um ein Problem der Gleichzeitigkeit, somit ist die Interpretation vom Bezugssystem abhängig.
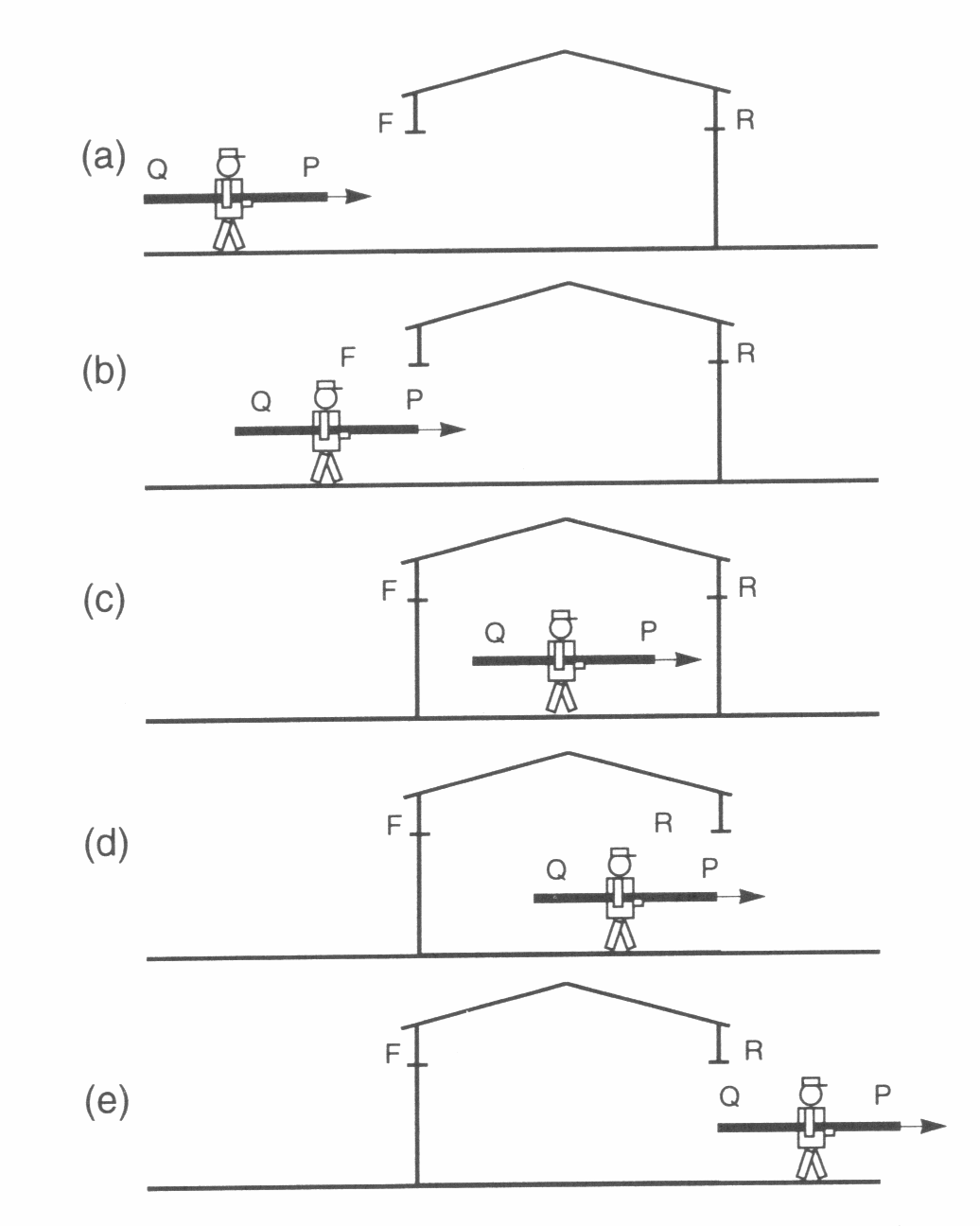
Man kann sich auch vorstellen, das Ein- und Austreten des Stabs sei mit dem Öffnen und Schließen der entsprechenden Türen der Scheune verbunden. Können also beide Türen geschlossen sein, wenn der Stab in der Scheune ist, oder nicht?
Der Stab hat also komplett in die Scheune gepasst.
Nun betrachten wir die Situation aus der Sicht des Stabs, also aus dem x',ct'-System. PF geschieht auch hier wieder als erstes. Mit Hilfe einer Parallelen zur x'-Achse (die gestrichelte blaue Linie) wird jedoch deutlich, dass das Austreten des Stabendes P aus der Tür R vor dem Eintreten des Stabendes Q in die Tür F liegt. Das heißt, das vordere Stabende verlässt die Scheune (PR) und erst dann passiert das Ende des Stabes die Eingangstür (QF), der Stab war demnach nie vollständig in der Scheune.
Es mag paradox klingen, dennoch sind beide Darstellungen richtig. Es handelt sich um ein Problem der Gleichzeitigkeit, somit ist die Interpretation vom Bezugssystem abhängig.
Man kann sich auch vorstellen, das Ein- und Austreten des Stabs sei mit dem Öffnen und Schließen der entsprechenden Türen der Scheune verbunden. Können also beide Türen geschlossen sein, wenn der Stab in der Scheune ist, oder nicht?
Das linke Bild zeigt, wie der Vorgang aus der Sicht der Scheune abläuft. Ganz offensichtlich sind die Türen F und R zum Zeitpunkt (c) beide gleichzeitig zu.
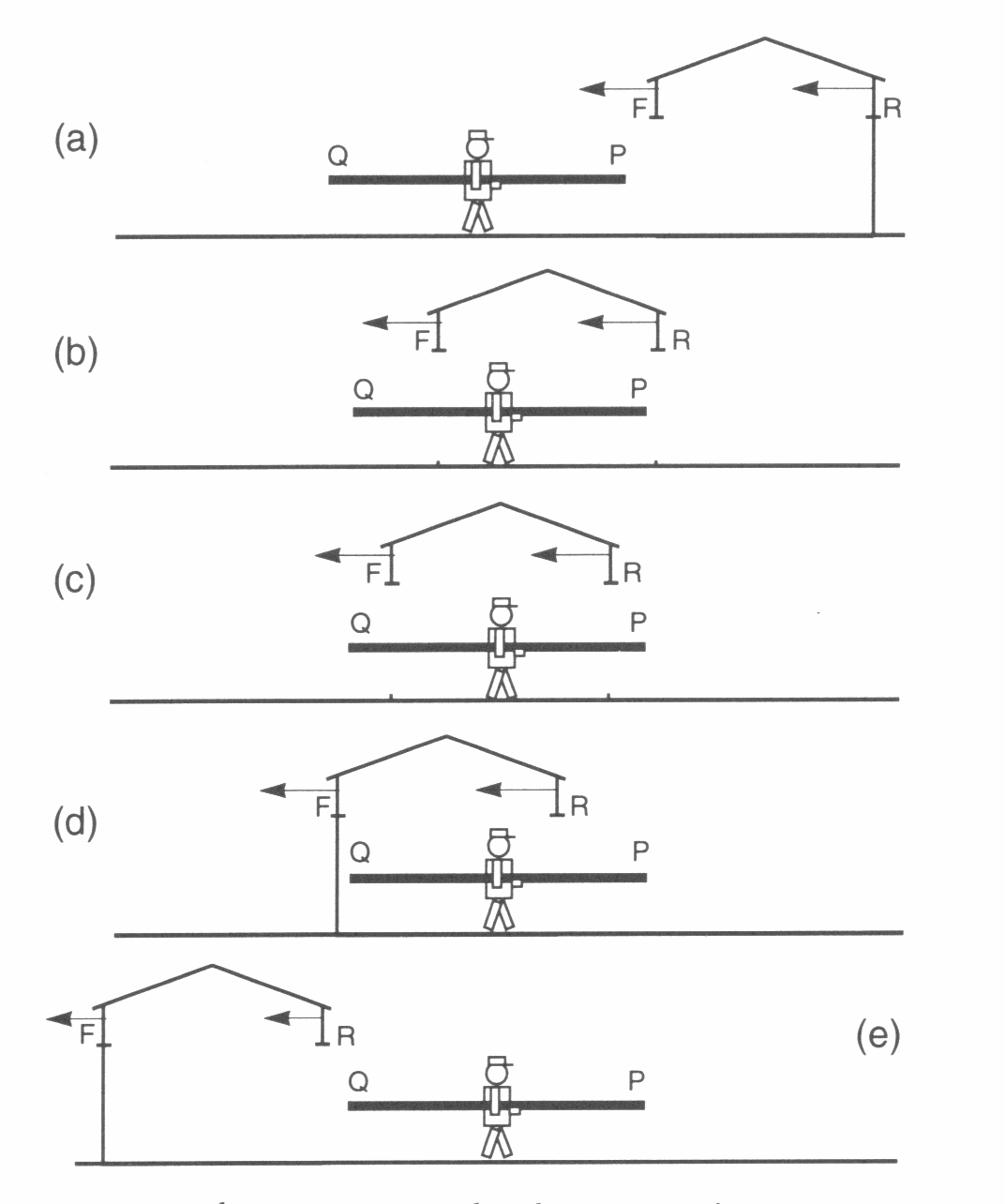
Das rechte Bild zeigt die Sicht des Läufers. Da hier das Ende P des Stabs die Scheune verlässt, bevor das Ende Q eintritt, muss die Tür R bereits aufgehen, bevor die Tür F zugeht. Die beiden Türen sind niemals gleichzeitig zu.
Aber das ist überhaupt kein Problem! Wir wissen, dass Gleichzeitigkeit nicht am selben Ort stattfindender Ereignisse nicht absolut ist. Es besteht also kein Grund anzunehmen, dass Scheune und Läufer die Frage, ob die Türen je gleichzeitig zu sind, in gleicher Weise beurteilen müssen. Die rote Gleichzeitigkeit ist nicht dieselbe wie die braune...
Diese Seite wurde von Sophie Seidenbecher während eines Schülerpraktikums erstellt.