3.5 Die Unsichtbarkeit der Lorentz-Kontraktion

Next: Zwillingsparadoxon    Up:Spezielle Relativitätstheorie   Previous: Längenkontraktion

In einer Geschichte zur Veranschaulichung der Längenkontraktion (von George Gamov: Mr. Thompkins seltsame Reisen durch Kosmos und Mikrokosmos) wird der Held in eine Welt versetzt, in der die Lichtgeschwindigkeit nur 30 km/s beträgt. Folglich sieht er die Radfahrer verkürzt und, als er selbst eine Zugfahrt macht, sehen alle Häuser um ihn herum verkürzt aus. Roman Sexl schreibt dann einen Nachsatz: "Was der Professor noch nicht wusste..."

Es ist nämlich so, dass die Längenverkürzung sich auf die tatsächliche Länge zu *einer* Zeit bezieht. Wenn wir einen ausgedehnten Gegenstand betrachten, sehen wir seine verschiedenen Teile aber gerade nicht, wie sie zu *einer* Zeit aussehen, sondern wir sehen weiter entfernte Teile, wie sie *früher* waren als näher liegende.

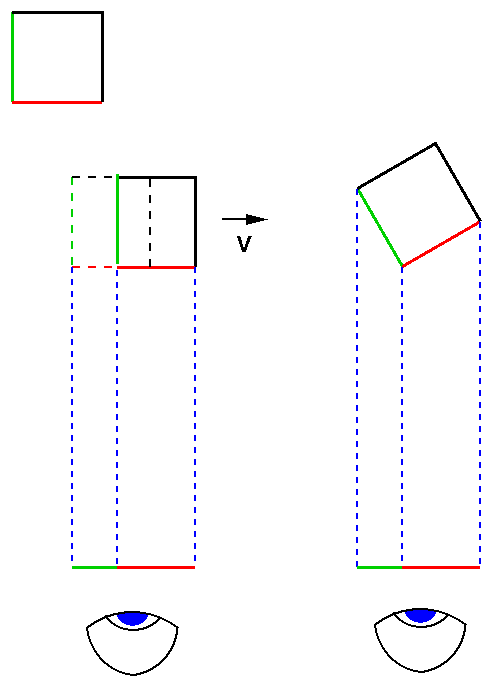
Das veranschaulicht das Bild. Links oben haben wir ein Quadrat, dessen linke Seite grün, die untere rot angemalt ist. Dieses Quadrat bewege sich mit einer konstanten Geschwindigkeit v nach rechts. Dabei wird es natürlich in der Richtung von v lorentzverkürzt. Die rote Seite wird kürzer. Die grüne ändert sich nicht.

Der Beobachter, dessen Auge unten gemalt ist, sieht also nach der Zeit, die das Licht von der roten Seite aus braucht, um bis zu ihm zu gelangen, die verkürzte rote Seite. Aber, und das ist der springende Punkt, er sieht auch die grüne Seite, denn in der Zeit, die das Licht von der linken oberen Ecke des Quadrates zur linken unteren braucht, hat sich dieses ja weiterbewegt, und so kommt Licht von allen grünen Punkten des Quadrates (ausgesandt zwischen der Zeit, in der das Quadrat die gestrichelte Lage einnahm und der, in der es die Lage mit den durchgezogenen Strichen hat) zu seinem Auge. Er sieht also von dem Quadrat einen grünen und einen roten Strich.

Rechts ist dargestellt, was der Beobachter von einem *ruhenden* aber *gedrehten* Quadrat sehen würde. Was dieses Bild suggeriert, ist richtig: der optische Eindruck ist *derselbe*, vorausgesetzt, man wählt den richtigen Drehwinkel (er ist durch sin a = v/c gegeben). Die Lorentzkontraktion wird optisch also nicht als Kontraktion sondern als *Drehung* wahrgenommen! Eine Kugel etwa behält Kugelgestalt. Damit ist die Kontraktion als solche unsichtbar.

Next: Zwillingsparadoxon   Up:Spezielle Relativitätstheorie   Previous: Längenkontraktion

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO