This page is available in English, too.
Diese Seite gibt es natürlich auch auf
deutsch.
Visites a cette page depuis 13 mars 1998.
Cette page est un peu passée de mode, mais elle mérite toujours d'être lue. Avant qu'une nouvelle vue d'ensemble soit créée, il faut se rapporter ma page scientifique pour une déscription de l'état actuel.
La croissance cristalline hors d'équilibre fournit une grande
richesse de phénomènes de formation de structures intéressantes.
Ainsi par exemple les alliages eutectiques solidifient sous forme
lamellaire, consistant de deux phases solides, mème aux températures
assez plus basses que le point eutectique.
Des structures à périodicité simple ont été
calculées en collaboration avec
C. Misbah de
l'Institut Laue-Langevin
et
l'Université Joseph Fourier.
Ce calcul qui peut être consideré standard aujourd'hui
a conduit à l'identification de
structures à parité brisée.
Les questions intéressantes qui se posent pour la continuation de notre recherche s'adressent à l'existence et la stabilité de structures plus complexes, dont des structures quasipériodiques et chaotiques en espace. En plus, il faudra explorer le comportement dynamique des systèmes non stationnaires. Ce deuxième type de problème en particulier va nécéssiter l'exploitation des ordinateurs jusqu'à la limite actuelle de leur capacité.
Nous nous intéressons plutôt à l'aspect fondamental des phénomènes de formation de structures. Quand même, nous espérons que les résultats attendus de cette recherche auront des utilisations sur le plan technologique. Un exemple bien connu, c'est les aubes de turbine modernes souvent faites en matériau eutectique ce qui leur rend une solidité supèrieure. Des résultats sur le domaine de stabilité de la croissance eutectique dans le diagramme de phase (la zone couplée) seraient sans doute désirables pour l'industrie.
Pour arriver à une grande solidité du matériau, on
essaie d'accélérer la solidification ; car il y a une règle
générale disant que plus vite ça solidifie, plus
fines seront les microstructures dans le matériau, et plus fine
est la ségrégation, plus solide sera le matériau...
(A l'extrème, on n'obtiendra plus de cristal mais plutôt
du verre, qui serait assez fort, normalement. Mais il est difficile
d'atteindre les vitesses nécessaires pour cela...)
Il y a quelques années, nous avons montré (suivant le travail de Brattkus et Davis), en collaboration avec des collègues français (de Grenoble) et, plus récemment, avec un groupe Suisse (de l'Ecole Polytechnique Fédérale de Lausanne), que la solidification en présence d'un gradient de température, c.a.d. la solidification dirigée obéit à des équations asymptotiques dans la limite de vitesses élevées. Ces équations sont des équations aux dérivées partielles et évidemment beaucoup plus simples que les équations intégral qu'il faut écrire d'habitude. Donc, la simulation numérique de systèmes tridimensionels d'une taille intéressante est devenue faisable pour la première fois.
Il est envisagé de comparer les résultats émanant
de ces simulations avec des expériences nouvelles du groupe de
B. Billia
à
Marseille.
Ces expériences ont rendu possible l'observation in situ
de la surface du cristal pendant la croissance tridimensionelle.
On trouve des structures cellulaires désordonnées
dont la charactérisation quantitative sera un des buts de notre
travail commun.
Récemment l'instabilité Grinfeld d'un solide qui
est soumis à des contraintes mécaniques
non hydrostatiques est devenue un
sujet favori parmi et les cristallers et les physiciens qui s'intéressent
à la formation de structures.
Cet intérêt renouvelé est dû au fait que,
l'instabilité étant connue dans la litterature
depuis plusieurs décennies, son caractère universel
- elle devrait affecter, en principe, tout solide
soumis à des contraintes uniaxiales -
n'a été aperçu qu'il y a quelques ans (1986).
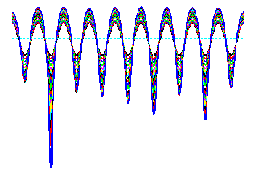
Un aspect frappant de cet instabilité, c'est qu'elle pourrait
fournir un mécanisme de la
génèse de fractures.
Nos études préliminaires indiquent que du moins dans
le cadre de la théorie d'élasticité linéaire
l'instabilité conduit à un état corrugué
dont l'amplitude s'amplifie indéfiniment. Cette amplification
s'accompagne de sillons aigus qui constituent un siège d'accumulation
spectaculaire de contraintes tangentielles qui peuvent éventuellement
atteindre le seuil de la fracture.
Or, un solide dans un gradient de température ou un alliage incorporant des impuretés va normalement se mettre dans un état contenant des contraintes locales. Des résultats de recherche récents ont montré que le couplage entre l'instabilité d'origine diffuse, importante dans la solidification dirigée, et l'instabilité élastique est fort et conduit à de phénomènes d'une nouvelle qualité. Nous nous proposons de suivre cette branche de recherche fascinante en collaboration avec des collègues de Grenoble et de Jülich.
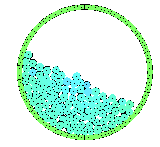Les propriétés de la matière granulaire
sont très différentes de celles des matériels "classiques".
Selon la situation dynamique, elle se comporte ou bien comme un solide ou
bien comme un fluide. Ni ses structures statiques complexes
ni sa dynamique ne sont bien comprises jusqu'ici.
Une différence importante entre les systèmes de granules
et de particules classiques, c'est la nature inélastique
des collisions entre les particules granulaires.
Dans l'étude de la formation de structures des fluides classiques on envisage de mieux comprendre les mécanismes non linéaires qui conduisent aux effets typiques de l'auto-organisation des structures. Quant aux milieux granulaires, le but est inversé : nous espérons mieux comprendre ces milieux "exotiques" via la formation de structures.
A Magdeburg, il y a un groupe expérimental, dont I. Rehberg est le directeur et qui font des expériences sur la formation de structures dans les milieux granulaires, et il y a un second groupe théorique avec des intérêts dans le domaine, dirigé par A. Engel. Donc il y a les meilleures conditions pour une collaboration fructueuse.
Nous envisageons de faire des simulations numériques modélisant ainsi réaliste que possible la dissipation dans les milieux granulaires. Comme point de départ nous prendrons des algorithmes développés par mon étudiant A. Schinner. Sa thèse de diplôme (hélas, en Allemand) mérite bien d'être lue.
ITP Homepage
AG Homepage
Stephan.Mertens@Physik.Uni-Magdeburg.DE
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO