Diese Seite gibt es natürlich auch auf deutsch.
Vous préférez français? Cliquez
ici.
Visits to this page since 17 Mai 2006.
This page is somewhat outdated, but still worth reading. Until a new global overview is generated, refer to my scientific homepage for a general survey.
Crystal growth under nonequilibrium conditions produces interesting
effects of pattern formation.
Eutectic alloys may, e.g., crystallize in lamellar structures consisting
of two solid phases even far from the eutectic point.
The calculation of stationary eutectic structures with a simple periodicity
unit, originally performed in collaboration with C. Misbah
of Institut Laue-Langevin
and Université Joseph Fourier,
both in Grenoble, has meanwhile become standard.
It led, among other things, to the identification of
parity-breaking patterns.
Interesting topics for future research include questions concerning the existence and stability of more complex structures, notably quasiperiodic and spatially chaotic ones, as well as the dynamic behaviour of nonstationary systems. Especially the second type of problem will require extensive numerical resources that are still at the borderline of currently available computer equipment.
We are mostly interested in fundamental aspects of pattern formation. Nonetheless we think that expected results of our research may not be devoid of industrial applicability. Composite eutectic materials have found application in the production of high-load turbine engines. Predictions about the stability range of eutectic growth (i.e., the coupled zone) would surely be of utmost interest to workers in the field of material engineering.
To obtain highly strain-resistant materials, people try to accelerate
solidification processes; there is a rule of thumb saying that segregation
microstructures of alloys get the finer the more rapidly the material
is solidified and that structural capacity improves with microstructures
becoming smaller.
(The extreme limit would be not a crystal but an amorphous solid, presumably
pretty strong as well. But these speeds are still beyond reach for most
bulk materials...) A few years ago, it was shown (following the work of Brattkus and Davis), in collaboration with French colleagues (from Grenoble) and more recently with a Swiss group (from EPFL Lausanne), that solidification in the presence of a temperature gradient, i.e. directional solidification, can be described by certain asymptotic equations in the high-speed limit. These equations are partial differential equations and thus simpler than the (nonlocal) integral equations ordinarily obtained in this context. Thus the numerical simulation of reasonably large three-dimensional systems has become feasible for the first time.
Our simulations will be compared with novel experiments developed in
Marseille
in the group of
B. Billia.
These experiments have rendered possible the in situ observation of
the crystal surface during three-dimensional growth.
What is found are disordered arrays of solidification cells, the
quantitative characterization of which will be one of the tasks of our
common work.
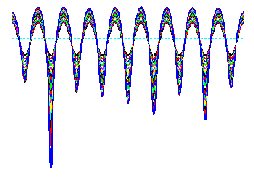Recently, the Grinfeld instability of solids that are subjected to
nonhydrostatic stress (or strain) has become a focus of interest both
to crystal growers and to physicists interested in pattern formation.
This renewed interest is due to the fact that, whereas the instability
has been known in
the literature for decades, its universal character
- in principle it is latently present in any
uniaxially strained solid - has not been
recognized until ten years ago (1986).
An interesting feature of this instability is that it might provide a
mechanism for the creation of cracks.
Preliminary research indicates that - at least within linear elasticity
the instability, once initiated, does not lead to a stationary state.
It generates grooves that just get deeper and deeper all the time, never
stopping.
During this process, tangential stresses at the crystal surface continue
to grow, possibly until the threshold of fracture.
Now any solid in a temperature gradient as well as an alloy incorporating impurities will most naturally reach a state with nonzero internal strain. It has only recently been realized that this gives rise to an interaction between diffusive instabilities, ubiquitous in directional solidification, and the elastic instability, and that this interaction is strong, leading to qualitatively novel phenomena. Research work in this direction will be continued together with scientists from Grenoble and Jülich.
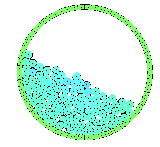Granular matter exhibits properties that make it very different from
"classical" materials.
Under varying dynamical conditions, it may behave like a solid or alternatively
like a fluid.
Neither the complex static arrangements nor the dynamics of granular media
are well understood.
There is an important difference between classical particle systems and
granular ones: in the latter collisions between particles are
inelastic.
Investigating pattern formation in classical fluids, people are interested in gaining a better understanding of the nonlinear mechanisms leading to self-organization of the structure. In granular media, the aim is reversed: we would like to learn via the detour or rather the means of studying pattern formation to improve our understanding of these "exotic" materials.
In Magdeburg, there is an experimental group, headed by I. Rehberg, looking at pattern formation phenomena in granular matter, and there is another theoretical group interested in the subject, headed by A. Engel. This should provide for ample possibilities of collaboration.
In our group, we would like to initiate numerical simulations that model dissipation by friction in these systems more realistically than has been done hitherto. These simulations will be based on algorithms developed by A. Schinner whose diploma thesis (in German, alas) is worth reading.
ITP Homepage
AG Homepage
Stephan.Mertens@Physik.Uni-Magdeburg.DE
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO