This page is available in English, too.
Vous préférez français? Cliquez
ici.
Besuche auf dieser Seite seit dem 17. Mai 2006.
Diese Seite ist etwas veraltet, wenngleich immer noch lesenswert. Bis zur Erstellung eines neuen globalen Überblicks muss der aus meiner wissenschaftlichen homepage hervorgehende Einblick genügen.
Kristallwachstum unter Nichtgleichgewichtsbedingungen führt zu
interessanten Strukturbildungseffekten. Eutektische Gemische können
z.B. auch bei Temperaturen fern vom eutektischen Punkt in lamellaren
Strukturen aus zwei festen Phasen kristallisieren.
Die Berechnung
einfach-periodischer stationärer Strukturen dieser Art,
die in Zusammenarbeit mit C. Misbah vom
Institut Laue-Langevin
und der
Université Joseph Fourier
in Grenoble durchgefürt wurde, ist mittlerweile
Standard. Sie hat unter anderem zur Identifikation von
paritätsbrechenden Strukturen geführt.
Interessant für die zuküftige Forschung ist die Frage der Existenz und Stabilität von komplexeren (quasiperiodischen, räumlich chaotischen) Strukturen, ferner die nach dem dynamischen Verhalten nichtstationärer Systeme. Insbesondere der zweite Problemkreis erfordert den Einsatz massiver numerischer Leistung, die durchaus noch im Grenzbereich heute verfügbarer Rechner liegt.
Während uns überwiegend der fundamentale Aspekt dieser Strukturbildungsphänomene interessiert, sind Anwendungsmöglichkeiten erhoffter Ergebnisse durchaus nicht aus der Welt. Hochfeste Turbinenschaufeln stellt man z.B. gern aus eutektischen Kompositmaterialien her, und Aussagen zum Stabilitätsbereich eutektischen Wachstums (der gekoppelten Zone) wären in der Industrie hochwillkommen.
Um hohe Materialfestigkeit zu erreichen, wendet man bei Erstarrungsprozessen
immer schnellere Verfahren an, denn eine Faustregel besagt, daß die
Mikrostrukturen im Material umso feiner werden, je schneller es kristallisiert,
und daß die Festigkeit umso größer ist, je feiner
die Mikrostrukturen sind... (Im Extremfall erhält man gar keinen
Kristall mehr sondern ein amorphes Material, das auch ganz schön fest ist.
Aber solche Geschwindigkeiten erreicht man selten...) Nun wurde in den letzten Jahren (auf der Grundlage einer Arbeit von Brattkus und Davis) in Zusammenarbeit mit französischen Kollegen (Grenoble) und einer Schweizer Gruppe (EPFL Lausanne) gezeigt, daß sich Kristallisation in einem Temperaturgradienten, auch gerichtete Erstarrung genannt, bei hohen Geschwindigkeiten mit verschiedenen asymptotisch gültigen einfacheren Gleichungen beschreiben läßt. Es handelt sich um partielle Differentialgleichungen statt der sonst üblichen (nichtlokalen) Integralgleichungen. Damit ist erstmals die Simulation größerer dreidimensionaler Systeme in den Bereich des Möglichen gerückt.
Diese Simulationen sollen mit neuen
Experimenten der Gruppe von
B. Billia
in
Marseille verglichen
werden, die die Beobachtung der Kristalloberfläche
während des Wachstumsprozesses
erlauben. Dabei treten ungeordnete Zellstrukturen auf, deren
quantitative Charakterisierung eines der Ziele unserer gemeinsamen
Arbeit sein wird.
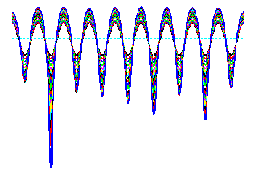Die Grinfeld-Instabilität eines Festkörpers, der einer
nichtisotropen mechanischen Spannung (oder Deformation) unterworfen wird,
ist neuerdings in den Mittelpunkt des Interesses sowohl von
Kristallzüchtern als auch von
Physikern, die sich mit Strukturbildung befassen,
gerückt. Das liegt daran, daß
obwohl die Instabilität selbst seit Jahrzehnten in der
Literatur bekannt ist, ihr universeller
Charakter - im Prinzip beeinflußt sie die Oberfläche
eines jeden Festkörpers, der uniaxiale Spannungen erfährt
- erst vor nicht allzulanger Zeit (1986) erkannt wurde.
Interessant an dieser Instabilität ist, daß
sie grundsätzlich einen Mechanismus darstellen könnte, der
zur Bildung von Rissen führt.
Erste Untersuchungen weisen darauf hin,
daß zumindest im Rahmen der linearen Elastizitätstheorie
die Instabilität, wenn sie einmal begonnen hat, nicht mehr zum
Stillstand kommt. Sie erzeugt Furchenstrukturen, die immer tiefer werden
und in denen die Tangentialspannungen an der Kristalloberfläche immer
weiter anwachsen, eventuell eben bis zur Rißgrenze.
Ein Festkörper in einem Temperaturgradienten oder eine Legierung, in die Fremdatome eingebaut werden, gerät mehr oder weniger automatisch in einen Zustand mit inneren mechanischen Spannungen. Es ist ebenfalls eine ziemlich neue Erkenntnis, daß die sich daraus ergebende Wechselwirkung zwischen diffusiven Instabilitäten, die bei gerichteter Erstarrung eine zentrale Rolle spielen, und der elastischen Instabilität stark ist und zu qualitativ neuen Erscheinungen führt. In dieser Richtung sollen Forschungen in Zusammenarbeit mit Wissenschaftlern aus Grenoble und Jülich weitergefürt werden.
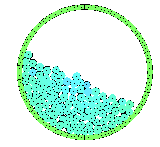Granulare Materie hat Eigenschaften, die sich wesentlich von denen
"klassischer" Materialien unterscheiden.
Sie verhält sich in verschiedenen dynamischen Situationen einmal wie
ein Festkörper, dann wieder wie ein Fluid.
Ihre komplexe Statik und
Dynamik ist noch weitgehend unverstanden.
Ein wichtiger Unterschied zu klassischen Teilchensystemen ist, daß
in granularen Medien Kollisionen zwischen Teilchen
inelastisch stattfinden.
Während man bei der Untersuchung von Strukturbildung in klassischen Fluiden hauptsächlich ein besseres Verständnis der nichtlinearen Mechanismen anstrebt, die zur Selbstorganisation von Strukturen führen, ist bei granularen Medien die Zielrichtung umgekehrt. Wir wollen über die Strukturbildung lernen, diese "exotischen" Materialien besser zu verstehen.
Im Hause werden von I. Rehberg und seiner Gruppe Strukturbildungsphänomene in granularen Medien experimentell untersucht, was eine Zusammenarbeit ebenso nahelegt wie die Tatsache, daß auch noch andere Theoretiker wie A. Engel sich für diese Effekte interessieren.
Ausgangspunkt für numerische Simulationen mit möglichst realistischer Modellierung der Dissipation in diesen Systemen sollen Algorithmen werden, die von meinem Mitarbeier A. Schinner entwickelt worden sind, dessen Diplomarbeit übrigens sehr lesenswert ist.
ITP Homepage
AG Homepage
Stephan.Mertens@Physik.Uni-Magdeburg.DE
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO