Institut für Physik
Kristallwachstum in einer Kapillare -- dynamische Strukturen
Dies sind Visualisierungen von Simulationen nichtfacettierten Kristallwachstums in einer hexagonalen Kapillare. Den Berechnungen wurde thermische Diffusion zugrundegelegt, mit gleichen Diffusionskonstanten in Festkörper und Flüssigkeit (symmetrisches Modell). Wegen der reflektierenden Randbedingungen ist der Benetzungswinkel an der Kapillarenwand 90 Grad. Bisher haben wir fünf oszillatorische Wachstumsmoden gefunden, die hier neben einer chaotischen dargestellt sind. Die visualisierten Simulationen sind mit isotroper Oberflächenspannung durchgeführt, aber zumindest die ersten beiden Moden, die chiralitätsbrechende und die Schaukelmode, existieren auch für schwache Anisotropie. Dass der pulsierende Einzelfinger ebenfalls mit Anisotropie existiert, ist sehr wahrscheinlich.
Rotierende Strukturen, Brechung der chiralen Symmetrie
Rotierender Doppelfinger, Δ=0.77, d0/L=0.007.
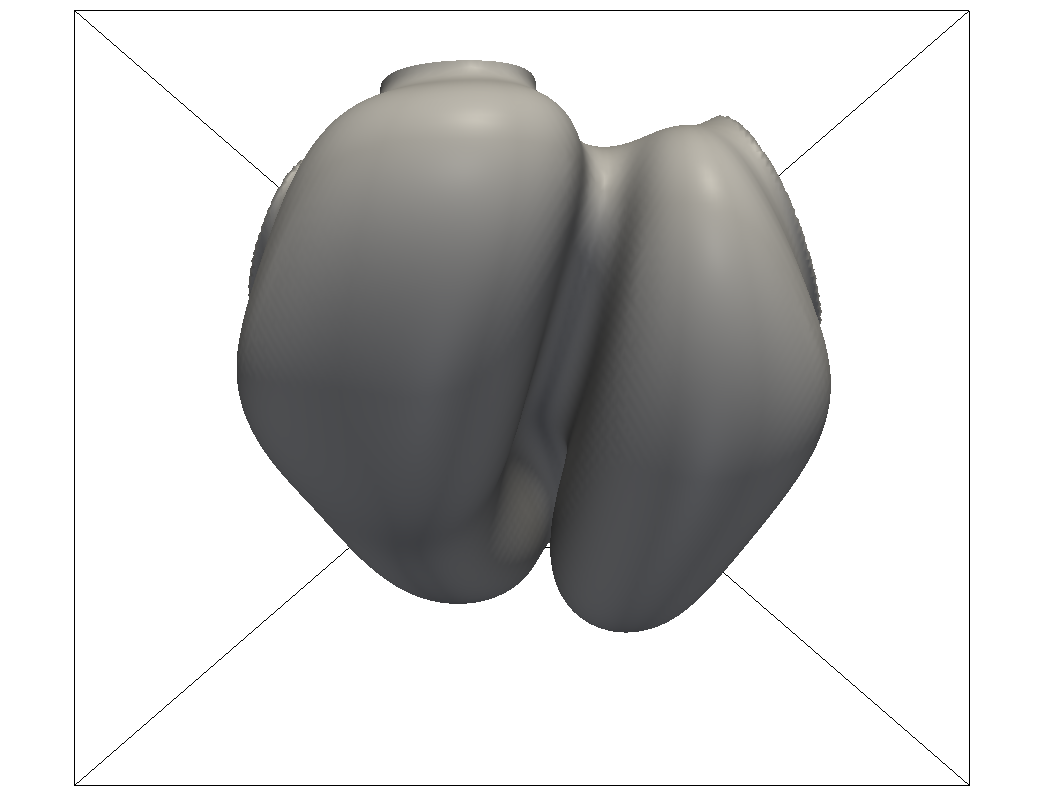
Rotierender Doppelfinger, Gegenrichtung, Δ=0.77, d0/L=0.007.
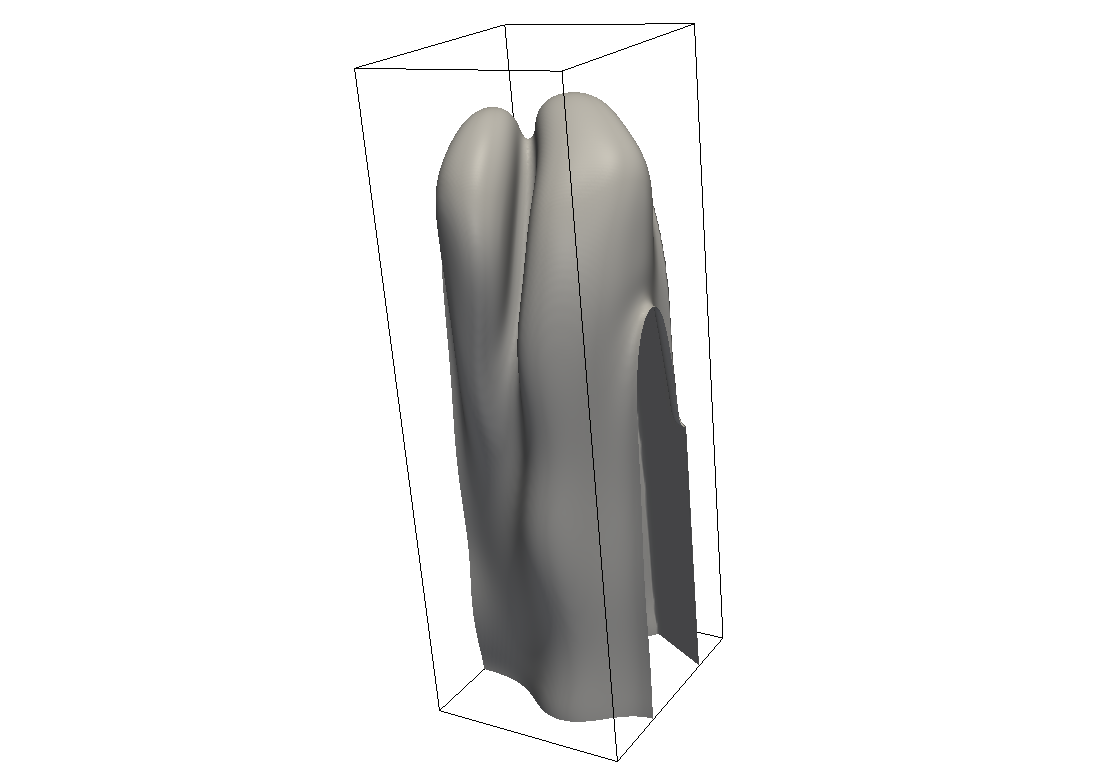
Rotierender Doppelfinger, Seitenansicht, Δ=0.77, d0/L=0.007.
Schaukelnde Strukturen
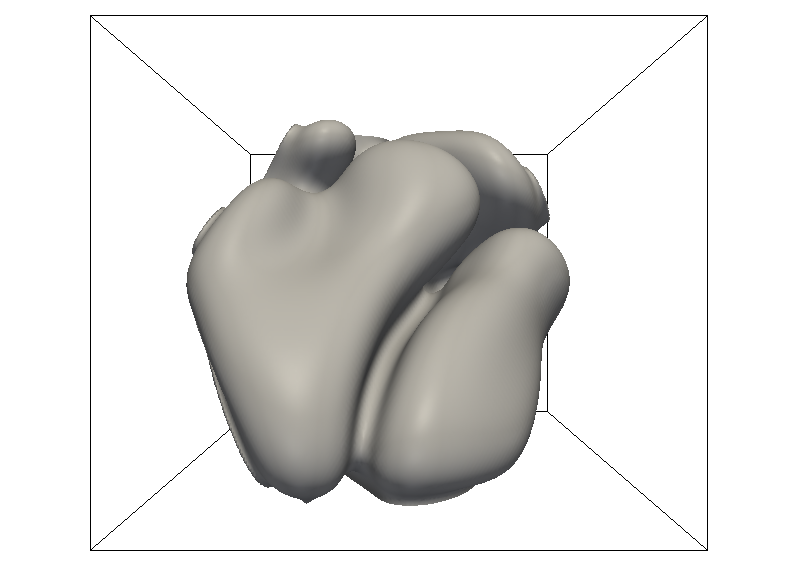
Schaukelnder Doppelfinger, Δ=0.80, d0/L=0.005.
Schaukelnder Doppelfinger, Seitenansicht, Δ=0.80, d0/L=0.005.
Pulsierender Finger
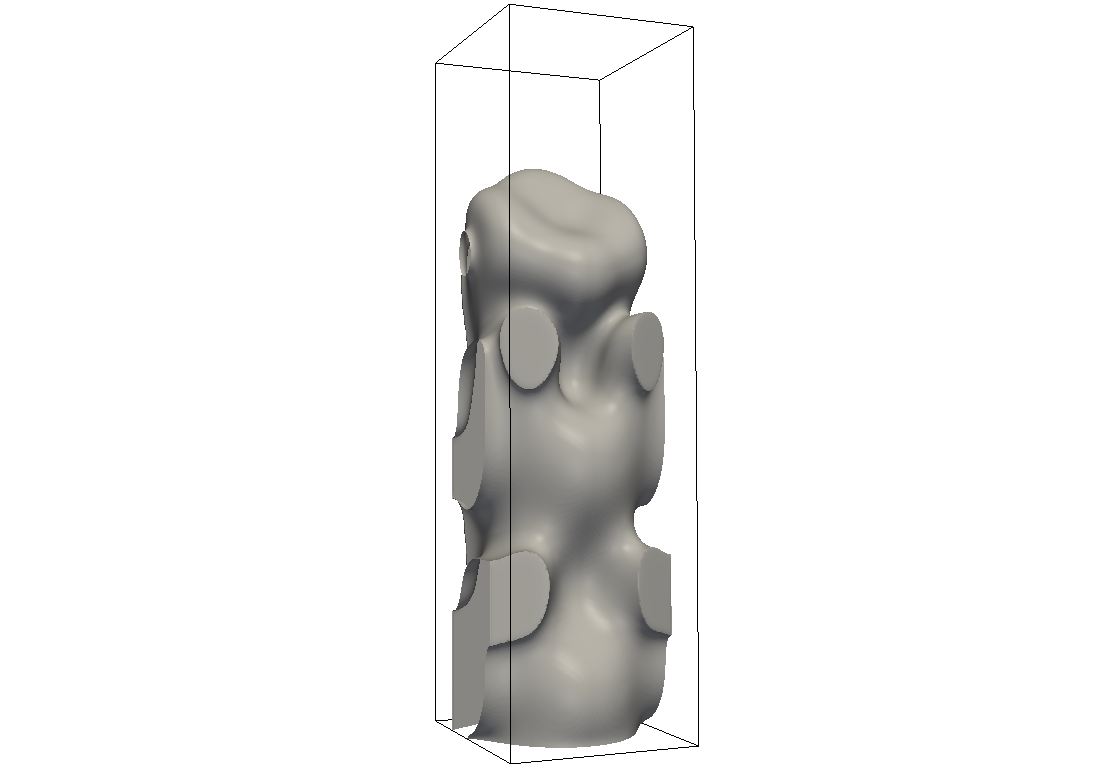
Pulsierender Finger, Δ=0.79, d0/L=0.007.
Pulsierender Finger, Draufsicht, Δ=0.79, d0/L=0.007.
Pulsierender Doppelfinger
Pulsierender Doppelfinger, Δ=0.67, d0/L=0.005.
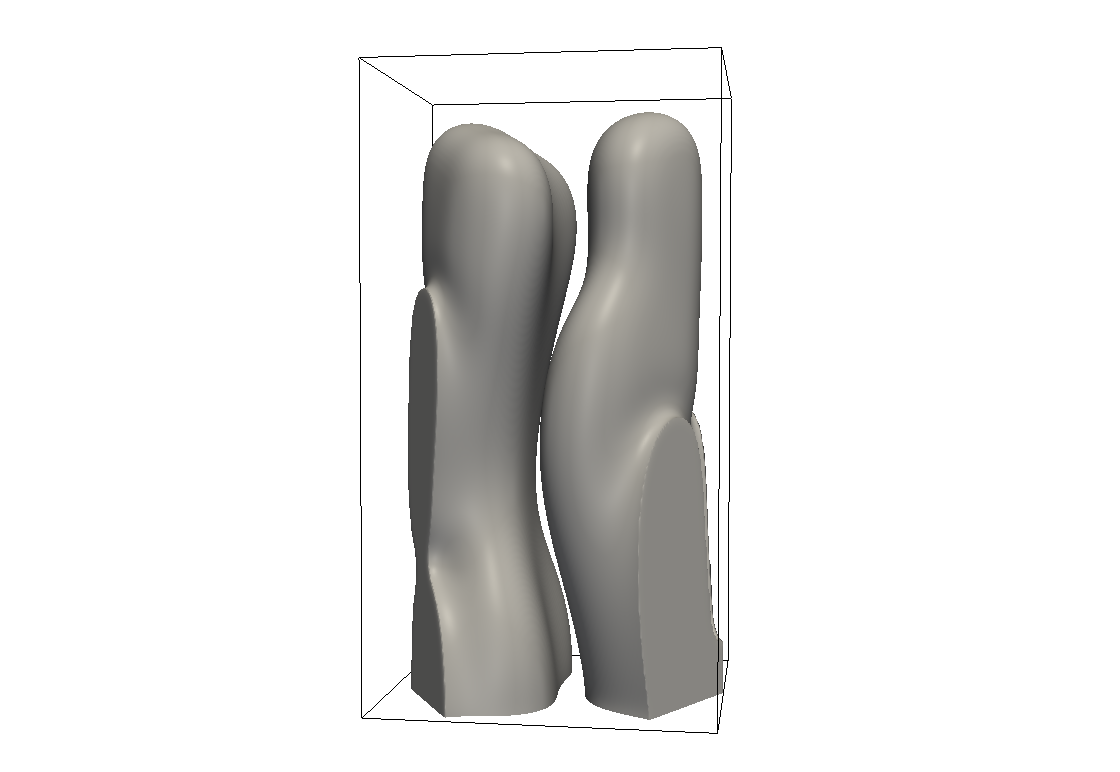
Pulsierender Doppelfinger, Seitenansicht, Δ=0.67, d0/L=0.005.
Pulsierender Vierfachfinger
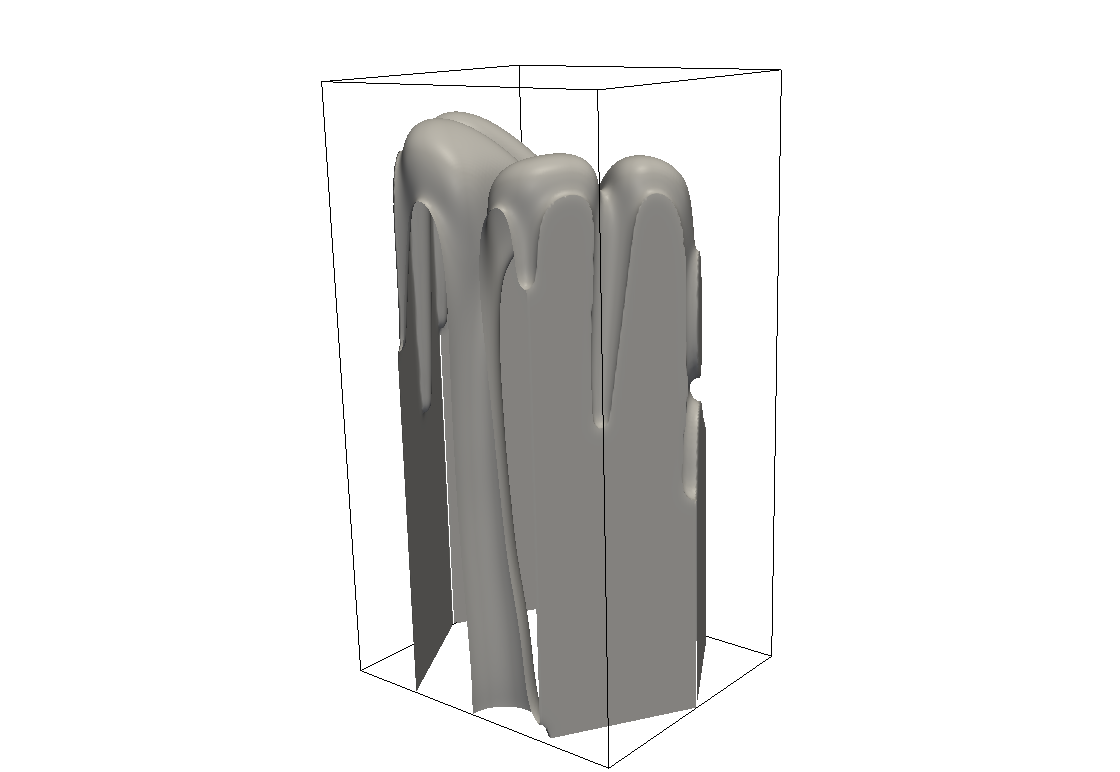
Pulsierender Vierfachfinger, Δ=0.79, d0/L=0.005.
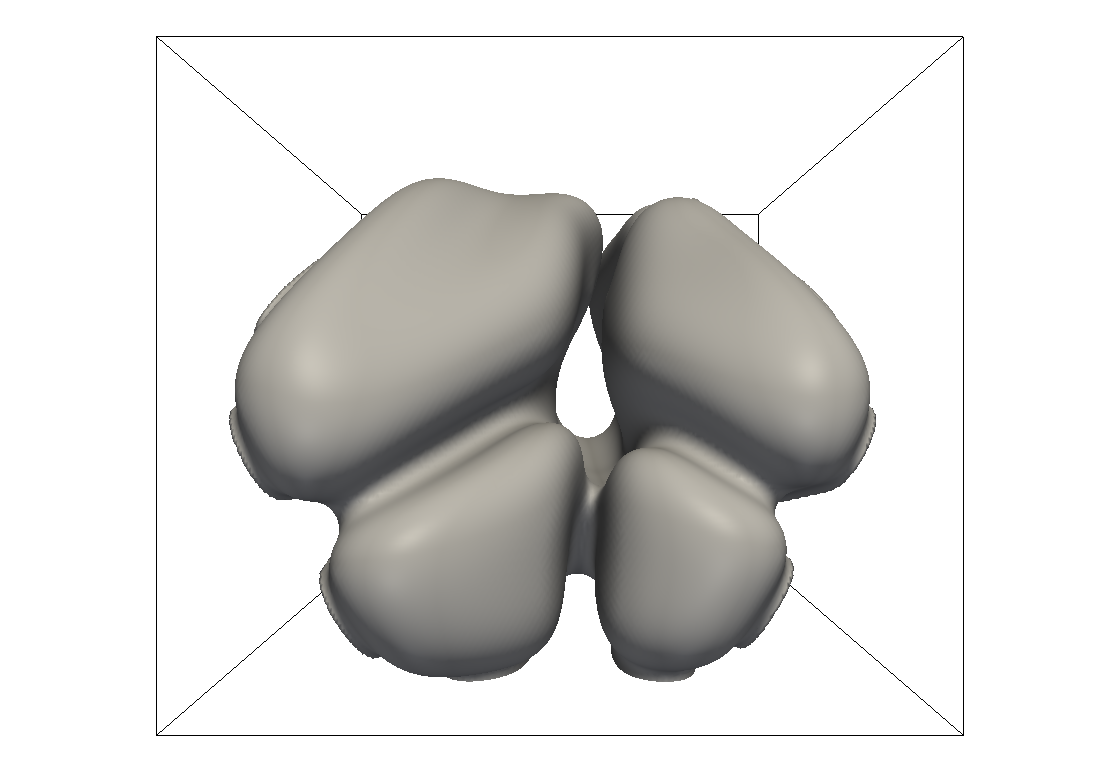
Pulsierender Vierfachfinger, Draufsicht, Δ=0.79, d0/L=0.005.
Chaotischer Finger
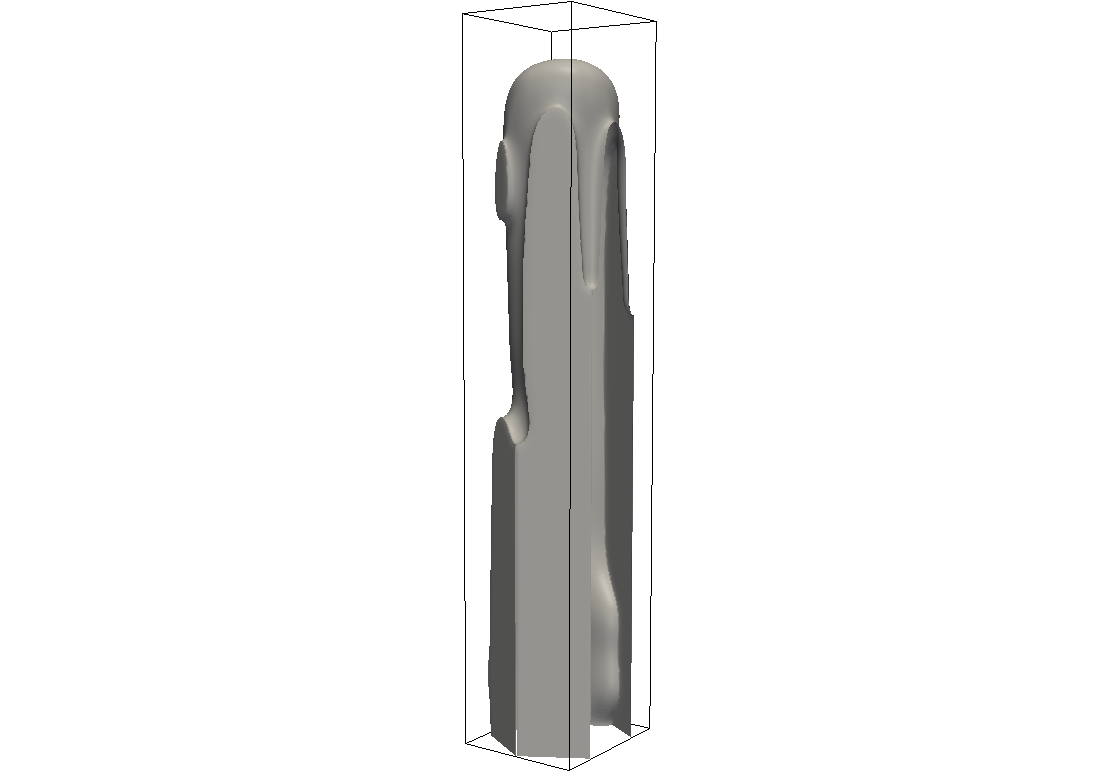
Chaotischer Finger, Δ=0.75, d0/L=0.01.
Chaotischer Finger, Draufsicht, Δ=0.75, d0/L=0.01.
 |
Otto-von-Guericke-Universität Magdeburg
FNW/ITP Prof. K. Kassner
PF 4120
D - 39016 Magdeburg
|
 |
Tel.: ++49 (0)391 67 18507
Fax.: ++49 (0)391 67 11205 |
ITP-Homepage
AG Stat. Phys.
Uni-Homepage
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO
Verantwortlich für diese Seite:
Klaus.Kassner@ovgu.de