DIRECTIONAL SOLIDIFICATION UNDER STRESS
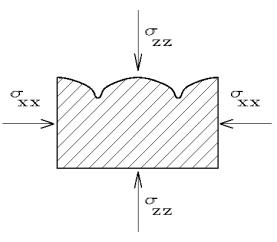 Fig. 1 Fig. 1
|
A non-hydrostatically strained solid in contact
with its own melt or vapor can partially relieve its elastic energy by
producing an undulated interface (Fig.1). This is the mechanism behind a morphological
instability of the interface giving rise to the evaluation of grooves with
a definite spacing under uniaxial stress and, possibly, island formation,
if the stress is biaxial. The instability
was first predicted by Asaro and Tiller [1].
Experimentally, it has been observed and studied by Torii and
Balibar[2].
Since the independent rediscovery of the
instability by Grinfeld [3],
it has often been referred to as the Grinfeld or Asaro-Tiller-Grinfeld instability (ATG).
Another better known surface instability is the Mullins Sekerka Instability in directional
solidification[4] (Fig. 2). Here a moving solidification front in an external temperature gradient
G undergoes a surface instability above a critical pulling velocity V. In principle one
can let V fixed and change G but for a controlled experiment G should be homogeneous and
changing V is simpler once one has a qualitatively good temperature gradient. The
instability can be sub- or supercritical depending on the partition coefficient k [5].
The planar interface bifurcates into a cellular structure (Fig.3). This structure can develop
to deep cells and at larger V to dendrites. In directional solidification the temperature gradient
acts like a very strong gravitational field bringing the length scale of the Grinfeld instability
in the range of the MS instability. Thus one can expect strong coupling between them [6].
A more detailed description can be found in my thesis [7].
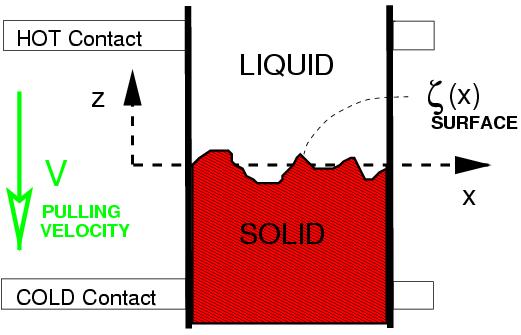 Fig. 2 Fig. 2
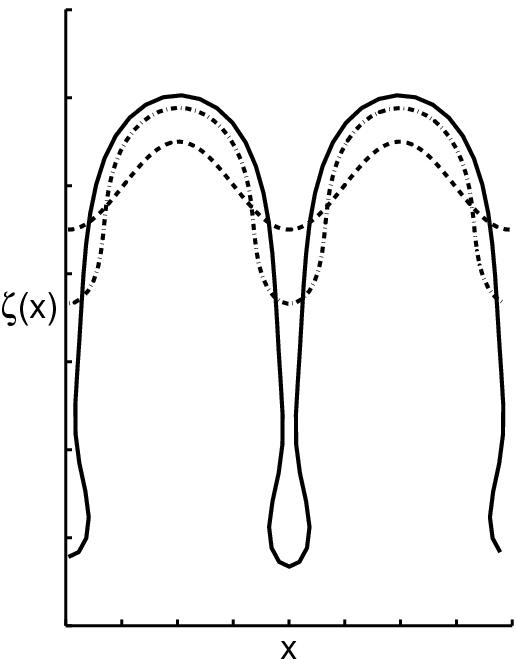 Fig. 3 Fig. 3
|
Some Definitions
Movies of the timedevelopement of the surface in a co-moving frame
In the beginning of the movie there is some information of parameters used for the calculation.
The most important parameter combinations are:
V/V_c = the ratio of the pulling velocity over the the velocity when MS comes into play,
\lambda/lambda_MS = the ratio of the wavelength of the pattern to the MS wavelength,
Peclet = the ratio of the wavelength to the diffusion length,
\eta = measure for the strength of the applied stress,
k_partition = the ratio of the slopes of liquidus and solidus lines
D_ratio = the ratio of the diffusivities in solid and liquid
Just Mullins Sekerka
| period 2 to period 3 |
A movie showing the development of a period 3 surface out of a period 2 one.
|
| ~1,3 Mb 380 frames |
Mullins Sekerka and applied Stress
| longer tails |
The black solid line is the steady state of the surface without applying stress. Turning on the stress lengthens the tails of the structure. The minimum of the surface goes down as one should expect because the stress acts mainly in the bottom parts and is leading there to a re-melting.
|
| ~0.5 Mb 90 frames |
References
[1] R. J. Asaro and W. A. Tiller, Metall. Trans. {\bf 3}, 1789 (1972).
[2] R.H. Torii and S. Balibar, J. Low Temp. Phys. {\bf 89}, 391 (1992).
[3] M.A. Grinfeld, Doklady Akademii Nauk SSSR {\bf 265} 836 (1982);
M.A. Grinfeld, Sov. Phys. Dokl. {\bf 31}, 831 (1986);
M.A. Grinfeld, Europhys. Lett. {\bf 22}, 723 (1993), and references therein.
[4] W.W. Mullins and R.F. Sekerka,J. Appl. Phys. {\bf 35},444 (1964)
[5] B. Caroli, C. Caroli, and B. Roulet, J. Phys (France) {\bf 43},1767 (1982)
[6] I. Cantat, K. Kassner, C. Misbah and H. Mueller-Krumbhaar, Phys. Rev. E {\bf 58},6026 (1998)
[7] J. Kappey, PhD thesis, Otto-von-Guericke Universität, Germany (2001)
Jens Kappey
Last modified: Mon Apr 2 19:42:03 GMT 2001
 Fig. 1
Fig. 1
 Fig. 1
Fig. 1
 Fig. 2
Fig. 2
 Fig. 3
Fig. 3