3.6 Das Zwillingsparadoxon

Eine Diskussion der speziellen Relativitätstheorie wäre ohne das Zwillingparadoxon unvollständig. Hier kommt es: Theresa und Stella sind Zwillinge, wobei Theresa einen etwas bodenständigeren Charakter hat, mehr auf Terra verwurzelt ist, während es Stella zu den Sternen zieht. Und sie nimmt die erste Gelegenheit wahr, um mit Mr. Ypsilon, der ein Raumschiff erproben will, nach Alpha Centauri zu fliegen, das sind ca. 4 Lichtjahre. Das Raumschiff wird praktisch dauernd mit v=4/5 der Lichtgeschwindigkeit fliegen, was, wenn man es nachrechnet, einen Zeitdilatationsfaktor von 3/5 gibt. Die Reise dauert also aus der Sicht von Ypsilon und Stella statt 5 nur 3 Jahre. Wenn sie zurückkommt, ist sie nur 6 Jahre älter als vorher, Theresa aber 10. Theresa grollt, als sie das hört.

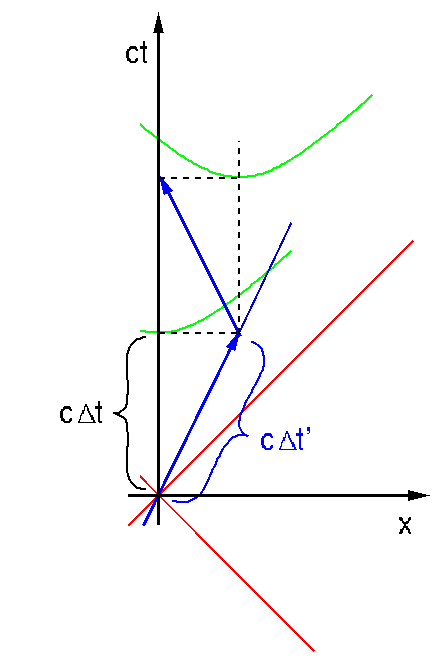
Das Diagramm macht die Situation klar. Stella bewegt sich entlang der durch die blauen Pfeile gegebenen Trajektorie. Auf der Erde vergeht zweimal die Zeit Δt, bis sie zurückkommt, während für Stella zweimal die Zeit  Δt' abläuft, und die Maßstabshyperbeln zeigen ganz klar, dass Δt' kleiner ist als Δt.      

Nun ist Theresa aber nicht dumm. Sie weiß, dass sich ja die Erde bezüglich des Raumschiffs bewegt, folglich muss aus Stellas Sicht natürlich während jedes der beiden Flüge Theresa langsamer altern als Stella. Also wird sie selbst bei Stellas Rückkehr die jüngere sein!

Wenn es tatsächlich so wäre, hätten wir ein ernstes Problem: Denn nach der Rückkehr können die beiden ihre Alterungserfahrungen (oder ihre Kalender) wirklich vergleichen, und es ist nicht gleichzeitig möglich, dass auf dem Kalender von Theresa weniger Tage abgehakt sind als auf dem von Stella *und* dass auf dem von Stella weniger Tage abgehakt sind als auf dem von Theresa. Das wäre *echt* paradox, in sich widersprüchlich. Und jedes Paradoxon muss ja seine Auflösung darin finden, dass es sich als nur scheinbar paradox erweist.

Nun, Stella lässt sich auch nicht ins Bockshorn jagen. Sie hat längst aufgezeichnet, wie der Flug aus ihrer Sicht aussieht. Das ist das nächste Diagramm. Während des Fluges in Richtung Centaurus vergeht für Theresa die Zeit Δt*, die tatsächlich kürzer ist als Δt', wie wieder die Maßstabshyperbel beweist. Während des Rückfluges ist es ebenso. Aber: die beiden Zeiten schließen sich nicht unmittelbar aneinander an, dazwischen ist eine Lücke! Denn Stella wechselt das Inertialsystem. Sie geht beim Umkehren über vom Bezugssystem (x' t') zum System (x" t"). Während des Umkehrvorgangs altert aus ihrer Sicht Theresa unheimlich schnell. Nach dem Umkehren altert sie wieder langsamer als Stella (aber sie holt den Zeitverlust bis zur Rückkehr nicht wieder ein).

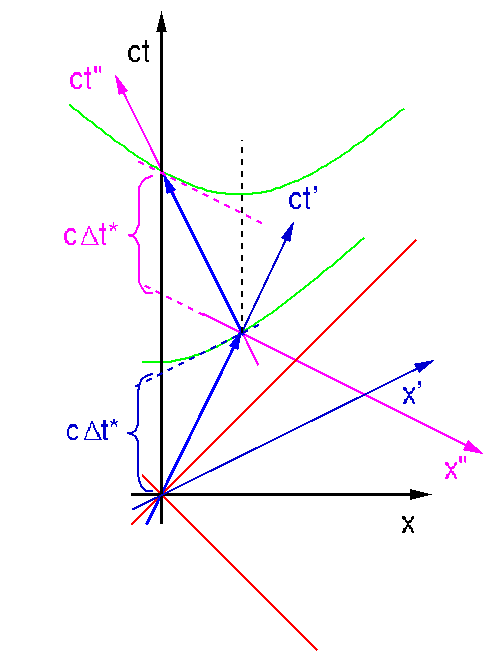Übrigens ist die Lücke, wie das Bild auch zeigt, abhängig von der *Entfernung* bei der Umkehr. Bei doppelt so großer Entfernung von der Erde aber gleichen Geschwindigkeitsverhältnissen wird sie doppelt so groß. Sie hat nichts mit der Stärke oder Dauer der *Beschleunigung* beim Umkehren zu tun.

Der Denkfehler ist also anzunehmen, dass die Situation der Zwillinge symmetrisch ist. Das ist sie nicht. Zwar verhalten sich die *relativen* Beschleunigungen der beiden symmetrisch zueinander [*], aber die von Stella ist mit einem echten Wechsel des Inertialsystems verbunden, merkbar an dem Andruck bei der Beschleunigung zwecks Bewegungsumkehr, während die von Theresa keinen Wechsel des Inertialsystems beinhaltet (als das die Erde hier näherungsweise angesehen wird). Sie merkt ja auch auf der Erde nichts von einer Bewegungsumkehr.

Hätten wir Drillinge, also etwa noch eine Ursula, die in der entgegengesetzten Richtung davonfliegt wie Stella, mit einem exakt symmetrischen Beschleunigungsprogramm, so wären bei der Rückkehr Ursula und Stella gleich alt (und beide jünger als Theresa). Dass tatsächlich Stella jünger bleibt, lässt sich ohne Rechnung nur aus dem  ersten Diagramm sehen, da wir beim zweiten ja nicht unmittelbar aus der Zeichnung entnehmen können, wie groß die Summe von 2 mal Δt* plus der Lücke im Vergleich zu 2 Δt' ist. Das zeigt, dass es im allgemeinen einfacher ist, Physik in Inertialsystemen zu beschreiben als in Nichtinertialsystemen (das Bezugssystem von Stella ist nicht über die gesamte Dauer der Reise inertial). Inertialsysteme können auch als solche Bezugssysteme definiert werden, in denen die physikalischen Gesetze eine besonders einfache Form haben.

[*] Kommentar 2012:
Da habe ich mich damals geirrt. In einer newtonschen Welt wären die relativen Beschleunigungen entgegengesetzt gleich. Relativistisch gesehen sind zwar die Geschwindigkeiten während der gleichförmig geradlinigen Bewegungen beider Zwillinge aus beider Sicht entgegengesetzt gleich. Aber schon das "während" in dieser Aussage ist suspekt. In der durch die Lücke definierten Zeitspanne Theresas hat Stella aus ihrer Sicht zwar immer eine wohldefinierte Geschwindigkeit v oder -v, bis auf das kurze Zeitintervall der Beschleunigung. Welche Geschwindigkeit soll Stella aber Theresa in dieser Zeitspanne zuordnen, die für sie selbst nur ganz kurz ist? Theresa erfährt in dieser Zeit aus Sicht Stellas eine Beschleunigung, aber die ist gerade anders herum gerichtet, als man es erwarten würde, und kann fantastische Werte erreichen. Während Stella verzögert, wird die Längenkontraktion der Strecke zur Erde schwächer, d.h. die Erde entfernt sich von ihr! Bis Stella zum Stillstand kommt, nimmt die Entfernung von etwas unter 2,4 Lichtjahren auf 4 Lichtjahre zu, Theresa entfernt sich also mit Überlichtgeschwindigkeit, wenn die Verzögerungsphase unter 1,6 Jahren dauert... Wenn Stella dann wieder beschleunigt, nimmt die Entfernung zur Erde wieder dramatisch ab, von 4 Lichtjahren zum Zeitpunkt des Stillstands auf unter 2,4 Lichtjahre, wenn sie die Geschwindigkeit -v erreicht hat. Die Erde rast also für einige Zeit überlichtschnell auf Stella zu!

Man kann offensichtlich nicht von Symmetrie der Beschleunigungen sprechen, denn aus Theresas Sicht ist Stella niemals solch drastischen Beschleunigungen ausgesetzt.  (Dass bei entgegengesetzt gleichen Geschwindigkeiten die Beschleunigungen nicht zwangsläufig gleich sein müssen, ist naheliegend, denn die Zeit, in der diese Geschwindigkeiten erreicht werden, ist für beide unterschiedlich. Dass aber so dramatische Effekte auftreten, das muss man sich erstmal durch den Kopf gehen lassen...)

Next: Tachyonenpistolenduell    Up:Spezielle Relativitätstheorie   Previous: Unsichtbarkeit Lorentz-Kontraktion