1. Newton
Klaus Kassner


Next: Elektrodynamik
Up:
Kurs
Previous:
Vorbemerkungen
In der Physik pflegt man Vorgänge in *Raum* und *Zeit* zu beschreiben.
Ein Kantianer könnte sagen, das sei notwendig so, da Raum und Zeit
Anschauungsformen unserer Vernunft seien, die Bedingungen objektiver Erkenntnis
sind und damit solcher Erkenntnis vorausgehen. Allerdings würde ein
"harter" Kantianer auch leugnen, dass Raum und Zeit selbst *Objekte* einer
physikalischen Theorie sein können. Die Physiker scheren sich nicht
drum und wir werden sehen, dass die spezielle Relativitätstheorie
letztlich eine Theorie der Struktur von Raum und Zeit ist. (Der Philosoph
hat allerdings einen Ausweg: Er kann behaupten, dass der Raum und die Zeit
der physikalischen Theorie nicht mit den uns a priori gegebenen Anschauungsformen von Raum und
Zeit identisch sind. Das wäre dann schon fast eine Lorentzsche Interpretation
der Relativitätstheorie. Aber dazu kommen wir noch.)
Zwecks Veranschaulichung der Beschreibung in Raum und Zeit benützt
man sogenannte Raum-Zeit-Diagramme. Der Einfachheit halber werde ich die
zunächst für die Newtonsche Mechanik diskutieren. Und weil man
vier Dimensionen (eine Zeit- und drei Raumdimensionen) so schlecht in
der Ebene zeichnen kann, werde ich in den meisten Bildern nur eine
Raumdimension benützen.
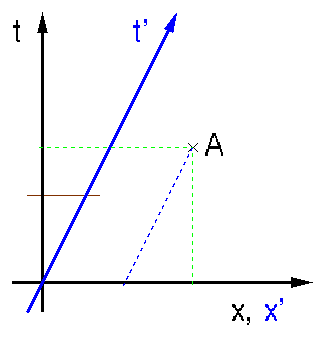 Das
nebenstehende Bild zeigt ein Raum-Zeit-Diagramm, wie man es in der Newtonschen
Mechanik benützen würde. Die Zeit-Achse (t) geht, vielleicht
ein bisschen ungewöhnlich, nach oben, die Raum-Achse (x) nach rechts.
Ein Punkt A in einem solchen Diagramm wird ein *Ereignis* genannt. Das
ist eine etwas vom üblichen Gebrauch des Wortes abweichende Definition.
Schlimmer noch, häufig gebrauchen Physiker (und ich mache da keine
Ausnahme) das Wort auch noch im üblichen Sinn, also als etwas, das
ein punktuelles Geschehen kennzeichnet. Das ist nicht ganz so fehlerträchtig
wie es den Anschein hat, denn wie sonst sollte man einen Punkt in Raum
und Zeit eindeutig kennzeichnen als durch etwas was dort gerade geschieht?
(Koordinatensysteme sind ja Geschmackssache.)
Das
nebenstehende Bild zeigt ein Raum-Zeit-Diagramm, wie man es in der Newtonschen
Mechanik benützen würde. Die Zeit-Achse (t) geht, vielleicht
ein bisschen ungewöhnlich, nach oben, die Raum-Achse (x) nach rechts.
Ein Punkt A in einem solchen Diagramm wird ein *Ereignis* genannt. Das
ist eine etwas vom üblichen Gebrauch des Wortes abweichende Definition.
Schlimmer noch, häufig gebrauchen Physiker (und ich mache da keine
Ausnahme) das Wort auch noch im üblichen Sinn, also als etwas, das
ein punktuelles Geschehen kennzeichnet. Das ist nicht ganz so fehlerträchtig
wie es den Anschein hat, denn wie sonst sollte man einen Punkt in Raum
und Zeit eindeutig kennzeichnen als durch etwas was dort gerade geschieht?
(Koordinatensysteme sind ja Geschmackssache.)
Nun betrachten wir ein Objekt oder einen Beobachter, der sich relativ
zu dem durch unser (xt)-System gekennzeichneten Bezugssystem mit einer
konstanten Geschwindigkeit bewegt. Solch eine Bewegung ist etwa durch den
blauen Pfeil gegeben. Eine derartige Linie im Raum-Zeit-Diagramm, die die
Bewegung eines Objekts beschreibt, nennt man *Weltlinie*. In unserem Fall
ist es wegen der angenommenen konstanten Geschwindigkeit eine Gerade, und
der Kehrwert ihrer Steigung entspricht der Geschwindigkeit.
Weshalb habe ich an den blauen Pfeil t' geschrieben? Nun, wenn es sich
um die Weltlinie eines Beobachters handelt, dann ist das auch gleichzeitig
die Zeitachse im Bezugssystem dieses Beobachters. Wieso? Die Zeitachse
ist ja der Ort aller Punkte mit einer festen Ortskoordinate (die t-Achse
ist durch x=0 gegeben). Für einen Beobachter, der sich entlang
der blauen Weltlinie bewegt, ist aber der Ort aller Punkte mit x'=0 gerade
diese Linie. Und so wie man die Koordinaten des Punkts A im System (xt)
durch Parallelprojektion auf die Achsen x und t erhält (grüne
gestrichelte Linien), so sind sie im System (x' t') durch Parallelprojektion
auf die Achsen x' und t' zu bestimmen. Da in der Newtonschen Mechanik die
Zeit absolut und für alle Beobachter gleich ist, ist die x'-Achse
(der Ort aller Punkte mit t'=0) identisch mit der x-Achse (dem Ort aller
Punkte mit t=0). Die Projektion ist also entlang der blauen gestrichelten
Linie entlang der waagerechten grünen durchzuführen.
Man sollte sich hier gleich klarmachen, dass aufgrund der Neigung der
t'-Achse der *Zeitmaßstab* im blauen Koordinatensystem ein anderer
ist als im schwarzen. Denn die Zeit t=t'=1 ist durch einen waagerechten
Schnitt (z.B. den schwarzen waagerechten Strich) gegeben, der offenbar
eine längeren Strecke auf der t'-Achse abschneidet als auf der t-Achse.
Wann immer wir mit solchen nicht rechtwinklig gezeichneten Koordinatensystemen
zu tun haben, werden wir uns mit solchen Maßstabsfragen befassen
müssen.
 Eine zentrale Aussage der Newtonschen Mechanik ist nun das *Relativitätsprinzip*
der Mechanik. Es besagt, dass durch kein denkbares *mechanisches* Experiment
feststellbar ist, mit welcher konstanten Geschwindigkeit man sich denn
nun bewegt. Anders ausgedrückt, alle konstanten Geschwindigkeiten
sind *relativ*, es gibt kein absolutes Bezugssystem, das einem erlauben
würde, eine Geschwindigkeit absolut festzulegen. Alle Geschwindigkeiten
sind nur bis auf einen beliebigen konstanten Wert definiert. Nochmal anders
ausgedrückt, der *Ort* ist keine absolute Größe. Die physikalischen
Gesetze haben für die Beobachter im (xt)-System und im (x' t')-System
genau die gleiche Form. Ein Objekt aber, das sich im (x' t')-System an
einem festen Ort (x') befindet, bewegt sich im (xt)-System (und umgekehrt).
Der Newtonsche Raum ist also durchaus nicht so absolut, wie das manchmal
geglaubt wird. Da alle mechanischen Gesetze unter den sogenannten *Galilei-Transformationen*
invariant sind -- das sind die mathematischen Beziehungen, die es erlauben,
von den Koordinaten eines sich mit konstanter Geschwindigkeit bewegenden
Koordinatensystems auf die eines anderen umzurechnen -- kann man dem Raum
nicht die Eigenschaft der Ruhe oder Bewegung zusprechen. Das gilt für
*geradlinige gleichförmige* Bewegungen (= konstante Geschwindigkeit).
Eine zentrale Aussage der Newtonschen Mechanik ist nun das *Relativitätsprinzip*
der Mechanik. Es besagt, dass durch kein denkbares *mechanisches* Experiment
feststellbar ist, mit welcher konstanten Geschwindigkeit man sich denn
nun bewegt. Anders ausgedrückt, alle konstanten Geschwindigkeiten
sind *relativ*, es gibt kein absolutes Bezugssystem, das einem erlauben
würde, eine Geschwindigkeit absolut festzulegen. Alle Geschwindigkeiten
sind nur bis auf einen beliebigen konstanten Wert definiert. Nochmal anders
ausgedrückt, der *Ort* ist keine absolute Größe. Die physikalischen
Gesetze haben für die Beobachter im (xt)-System und im (x' t')-System
genau die gleiche Form. Ein Objekt aber, das sich im (x' t')-System an
einem festen Ort (x') befindet, bewegt sich im (xt)-System (und umgekehrt).
Der Newtonsche Raum ist also durchaus nicht so absolut, wie das manchmal
geglaubt wird. Da alle mechanischen Gesetze unter den sogenannten *Galilei-Transformationen*
invariant sind -- das sind die mathematischen Beziehungen, die es erlauben,
von den Koordinaten eines sich mit konstanter Geschwindigkeit bewegenden
Koordinatensystems auf die eines anderen umzurechnen -- kann man dem Raum
nicht die Eigenschaft der Ruhe oder Bewegung zusprechen. Das gilt für
*geradlinige gleichförmige* Bewegungen (= konstante Geschwindigkeit).
Dass dem Newtonschen Raum durchaus eine feste *Rotationsgeschwindigkeit*
(z.B. Null) zugesprochen werden kann, zeigt das berühmte Newtonsche
Eimerexperiment. Wenn man einen Eimer mit Wasser rotieren lässt, dann
wird sich nach einer Weile ein Gleichgewichtszustand der Wasseroberfläche
in der Form eines Rotationsparaboloids einstellen. Aus dem Krümmungsradius
dieses Paraboloids im Zentrum kann auf die Rotationsgeschwindigkeit des
Eimers gegenüber dem "absoluten Raum" geschlossen werden. Ist die
Krümmung Null, d.h. die Oberfläche eben, rotiert der Eimer nicht.
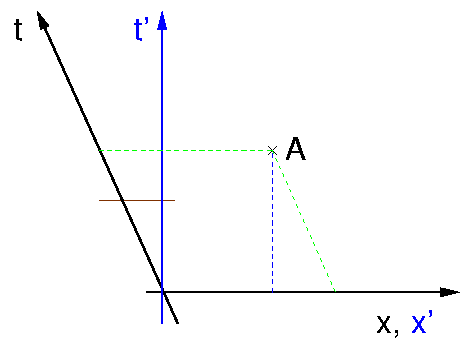
Für
geradlinige gleichförmige Bewegungen aber gilt das Relativitätsprinzip,
d.h. unser schwarzer und blauer Beobachter sind völlig gleichberechtigt.
Jeder kann sich zu Recht als in Ruhe befindlich
betrachten. Zwar bevorzugt unsere Darstellung den schwarzen Beobachter,aber
das lässt sich leicht ändern, wie das Bild rechts zeigt, dessen
Informationsgehalt natürlich genau der gleiche ist wie der
des ersten Bilds. Aber jetzt haben wir dem blauen Beobachter rechte
Winkel zugebilligt.
Next: Elektrodynamik
Up:
Kurs
Previous:
Vorbemerkungen
Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO
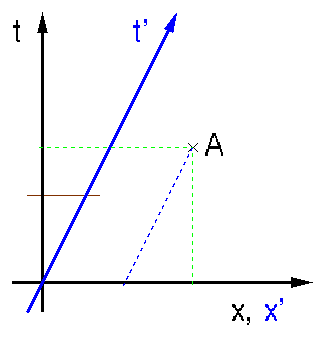 Das
nebenstehende Bild zeigt ein Raum-Zeit-Diagramm, wie man es in der Newtonschen
Mechanik benützen würde. Die Zeit-Achse (t) geht, vielleicht
ein bisschen ungewöhnlich, nach oben, die Raum-Achse (x) nach rechts.
Ein Punkt A in einem solchen Diagramm wird ein *Ereignis* genannt. Das
ist eine etwas vom üblichen Gebrauch des Wortes abweichende Definition.
Schlimmer noch, häufig gebrauchen Physiker (und ich mache da keine
Ausnahme) das Wort auch noch im üblichen Sinn, also als etwas, das
ein punktuelles Geschehen kennzeichnet. Das ist nicht ganz so fehlerträchtig
wie es den Anschein hat, denn wie sonst sollte man einen Punkt in Raum
und Zeit eindeutig kennzeichnen als durch etwas was dort gerade geschieht?
(Koordinatensysteme sind ja Geschmackssache.)
Das
nebenstehende Bild zeigt ein Raum-Zeit-Diagramm, wie man es in der Newtonschen
Mechanik benützen würde. Die Zeit-Achse (t) geht, vielleicht
ein bisschen ungewöhnlich, nach oben, die Raum-Achse (x) nach rechts.
Ein Punkt A in einem solchen Diagramm wird ein *Ereignis* genannt. Das
ist eine etwas vom üblichen Gebrauch des Wortes abweichende Definition.
Schlimmer noch, häufig gebrauchen Physiker (und ich mache da keine
Ausnahme) das Wort auch noch im üblichen Sinn, also als etwas, das
ein punktuelles Geschehen kennzeichnet. Das ist nicht ganz so fehlerträchtig
wie es den Anschein hat, denn wie sonst sollte man einen Punkt in Raum
und Zeit eindeutig kennzeichnen als durch etwas was dort gerade geschieht?
(Koordinatensysteme sind ja Geschmackssache.)
 Eine zentrale Aussage der Newtonschen Mechanik ist nun das *Relativitätsprinzip*
der Mechanik. Es besagt, dass durch kein denkbares *mechanisches* Experiment
feststellbar ist, mit welcher konstanten Geschwindigkeit man sich denn
nun bewegt. Anders ausgedrückt, alle konstanten Geschwindigkeiten
sind *relativ*, es gibt kein absolutes Bezugssystem, das einem erlauben
würde, eine Geschwindigkeit absolut festzulegen. Alle Geschwindigkeiten
sind nur bis auf einen beliebigen konstanten Wert definiert. Nochmal anders
ausgedrückt, der *Ort* ist keine absolute Größe. Die physikalischen
Gesetze haben für die Beobachter im (xt)-System und im (x' t')-System
genau die gleiche Form. Ein Objekt aber, das sich im (x' t')-System an
einem festen Ort (x') befindet, bewegt sich im (xt)-System (und umgekehrt).
Der Newtonsche Raum ist also durchaus nicht so absolut, wie das manchmal
geglaubt wird. Da alle mechanischen Gesetze unter den sogenannten *Galilei-Transformationen*
invariant sind -- das sind die mathematischen Beziehungen, die es erlauben,
von den Koordinaten eines sich mit konstanter Geschwindigkeit bewegenden
Koordinatensystems auf die eines anderen umzurechnen -- kann man dem Raum
nicht die Eigenschaft der Ruhe oder Bewegung zusprechen. Das gilt für
*geradlinige gleichförmige* Bewegungen (= konstante Geschwindigkeit).
Eine zentrale Aussage der Newtonschen Mechanik ist nun das *Relativitätsprinzip*
der Mechanik. Es besagt, dass durch kein denkbares *mechanisches* Experiment
feststellbar ist, mit welcher konstanten Geschwindigkeit man sich denn
nun bewegt. Anders ausgedrückt, alle konstanten Geschwindigkeiten
sind *relativ*, es gibt kein absolutes Bezugssystem, das einem erlauben
würde, eine Geschwindigkeit absolut festzulegen. Alle Geschwindigkeiten
sind nur bis auf einen beliebigen konstanten Wert definiert. Nochmal anders
ausgedrückt, der *Ort* ist keine absolute Größe. Die physikalischen
Gesetze haben für die Beobachter im (xt)-System und im (x' t')-System
genau die gleiche Form. Ein Objekt aber, das sich im (x' t')-System an
einem festen Ort (x') befindet, bewegt sich im (xt)-System (und umgekehrt).
Der Newtonsche Raum ist also durchaus nicht so absolut, wie das manchmal
geglaubt wird. Da alle mechanischen Gesetze unter den sogenannten *Galilei-Transformationen*
invariant sind -- das sind die mathematischen Beziehungen, die es erlauben,
von den Koordinaten eines sich mit konstanter Geschwindigkeit bewegenden
Koordinatensystems auf die eines anderen umzurechnen -- kann man dem Raum
nicht die Eigenschaft der Ruhe oder Bewegung zusprechen. Das gilt für
*geradlinige gleichförmige* Bewegungen (= konstante Geschwindigkeit).