3.4 Die Längenkontraktion (Lorentz-Kontraktion)

Next: Unsichtbarkeit Lorentz-Kontraktion   Up: Spezielle Relativitätstheorie   Previous: Zeitdilatation

Das nächste Bild befasst sich mit der Frage von Längenmessungen.

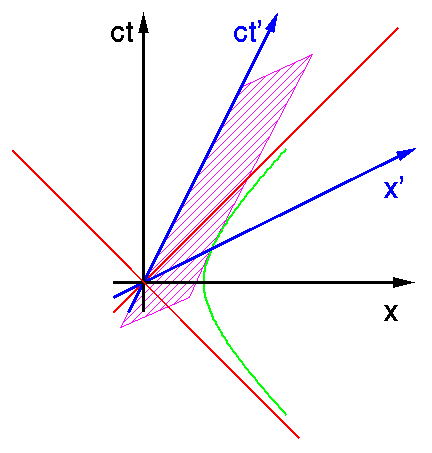Das schraffierte Parallelogramm stellt die Weltlinien eines im blauen System ruhenden Meterstabs dar. Wie lang ist dieser Stab im schwarzen System?

Die Frage ist a priori gar nicht so einfach zu beantworten. Denn im schwarzen System bewegt sich der Stab ja. Versucht man also, seine Länge mit einem Maßband zu messen, so wird eine gewisse Zeit zwischen dem Anlegen des Maßbands an seinem einen Ende und dem Erreichen des anderen Endes vergehen, das sich inzwischen aber weiterbewegt hat. Der gemessene Abstand der beiden Enden ist dann natürlich nicht die Länge des Stabs. Um die wirkliche Länge herauszubekommen, muss man also die Position der beiden Enden zu *einem* Zeitpunkt kennen. Das kann man etwa erreichen, indem man eine Menge Beobachter (die relativ zum schwarzen System ruhen) entlang der x-Achse aufstellt; die beiden Beobachter, bei denen zur Zeit t=0 ein Stabende ist, ritzen dort, wo es sich befindet, eine Kerbe in den Boden. Dann kann man in aller Ruhe den Abstand der beiden Kerben messen. Wenn aber die Längenbestimmung so eng mit der Zeitbestimmung verknüpft ist, nimmt es nicht weiter wunder, dass verschiedene Beobachter zu verschiedenen Resultaten kommen.

So ist es auch. Man kann dem Bild sofort entnehmen, dass die beiden Schnittpunkte der Weltlinien der Stabenden mit der x-Achse *näher* beeinander liegen als die Stabenden im (x' t')-System; denn der Abstand 1 m vom Ursprung ist ja durch die grüne Hyperbel bestimmt. Der bewegte Maßstab ist also im schwarzen System *kürzer* als im blauen, deshalb spricht man von Längenkontraktion.

Angenommen, die Verkürzung reduziert die Länge des Stabs im schwarzen System auf 80 cm. Wenn wir dann zu dem Zeitpunkt (im schwarzen System), zu dem sein eines Ende den Ursprung (x=0, t=0) passiert, entlang der gesamten x-Achse mit Ausnahme eines "Lochs", das von x=-5cm bis x= 85cm geht, Laserstrahlen zünden (die z.B. parallel zur nicht gezeichneten y-Achse laufen), so wird der Stab das Loch ohne weiteres durchfliegen, da er ja kürzer als 90 cm ist. Die Laserstrahlen sollen unmittelbar danach wieder abgeschaltet werden.

Nun sehen wir uns eine ähnliche Situation an, bei der ein Stab im (xt)-System ruht. Seine Länge im blauen System, gegeben durch die Schnittpunkte mit der x'-Achse, ist offenbar ebenfalls *kürzer* als die Länge im schwarzen System. Wir haben also wieder eine symmetrische Situation. Jeder Beobachter stellt fest, dass Längen im anderen System kürzer sind als im eigenen.

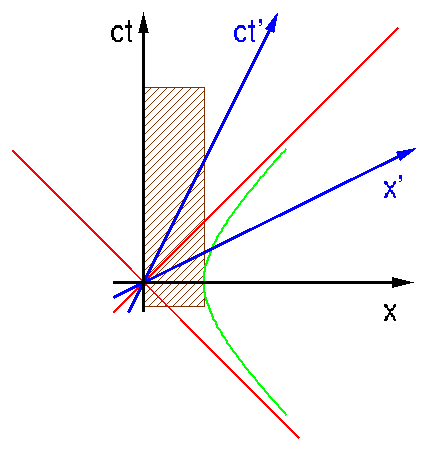Gibt das mit unserem Loch in einer Wand aus Laserstrahlen kein Problem? Vom bewegten Stab aus, der sich im blauen System befindet (erstes Bild), ist seine eigene Länge ja 1 m, die des Lochs sollte hingegen kürzer sein als die 90 cm, die im schwarzen System gemessen werden... Die Laserstrahlen sollten also die Enden des zu langen Stabs abschneiden...

Das wäre in der Tat eine paradoxe Situation. Aber so ist es natürlich nicht. Denn für den Stab im blauen System (erstes Bild) zünden die Laserstrahlen *nicht* gleichzeitig. Was aus seiner "Sicht" passiert, ist, dass die Laserstrahlen für sehr große x-Werte sehr früh zünden. Dann nähert sich die Laserfront (überlichtschnell!) bis kurz *vor* dem Zeitpunkt, zu dem sein Vorderende die x-Achse passiert. Dann gehen die Laser aus und nach einer Pause auf der negativen x-Achse wieder an, von wo sich die Laserfront zu negativen x-Werten hin entfernt. Die Laser gehen aber erst an, *nachdem* das Hinterende des Stabs die x-Achse passiert. Zu diesem Zeitpunkt ist sein Vorderende dort, wo vorher Laserstrahlen waren. Das heißt, der Stab ist wohl länger als der kürzeste Abstand der Laserfeuer, aber sein Vorderende geht vor seinem Hinterende durch das "Loch" und zwar gerade so, dass es die Laser vermeidet.

Vom blauen System aus gesehen, ist gar kein räumliches Loch da, sondern nur eine Laserfront, die ausgeht, knapp bevor sie passiert wird und wieder an, nachdem man vorbei ist.

So ist auch Minkowskis Zitat zu verstehen, "Raum für sich selbst und Zeit für sich selbst werden in bloße Schatten versinken, und nur eine Art Vereinigung zwischen ihnen wird überleben": das Loch, das im einen System eine rein räumliche Distanz verkörpert, ist im anderen eine Kombination aus einer (kürzeren) räumlichen und einer zeitlichen Distanz.

Nun kommt es schon mal vor, dass ein "Relativist" ein bisschen darauf herumreitet, dass die Längenkontraktion *nur* eine Folge unserer Konventionen zum Längenmessen sei. So ganz und gar falsch ist das nicht, denn wenn wir übereinkämen, Längen bewegter Objekte nicht als "Längen zu einer festen Zeit" zu messen, so hätten wir nicht notwendigerweise eine relativistische Längenkontraktion. Aber es ist eigentlich keine andere vernünftige Konvention zu sehen (Konventionen mögen beliebig sein, aber ihre Nützlichkeit hängt sehr wohl von ihrem Inhalt ab). Und es folgt aus der Abhängigkeit der Längenkontraktion von der Messvorschrift für Längen eben *nicht*, dass sie irgendwie nicht *real* sei.

Das zeigt sehr schön das Raumschiffparadoxon von John Bell (ja, dem berühmten, der die Bellschen Ungleichungen abgeleitet hat):

Man stelle sich zwei Raumschiffe vor, die bezüglich eines festen Beobachters exakt das gleiche Beschleunigungsprogramm haben, so dass ihr Abstand gleich bleibt, während ihre Geschwindigkeit kontinuierlich zunimmt. Zwischen den Raumschiffen sei ein Seil gespannt, das genau die Länge ihres Abstands hat. Es soll kein besonders starkes Seil sein, so dass es die Beschleunigungen der Raumschiffe nicht beeinflusst.

Reißt das Seil oder reißt es nicht? Dafür, dass es nicht reißt, spricht, dass seine Länge fest bleibt. Dafür, dass es reißt, spricht, dass es ja eigentlich eine Lorentzkontraktion machen müsste. Dieses Puzzle wurde von Kennern der Relativitätstheorie auch schon falsch gelöst (auf die Schnelle, im nachhinein verstehen sie es dann schon). Die Antwort kommt in Abschnitt 3.8.

Dieses Beispiel ist auch geeignet klarzumachen, dass die spezielle Relativitätstheorie nicht auf Objekte beschränkt ist, die sich mit konstanter Geschwindigkeit bewegen. Man kann durchaus beschleunigte Systeme damit behandeln. Die Beschreibung innerhalb der Theorie erfolgt aus der Sicht eines unbeschleunigten *Beobachters*. Das heißt, sie beschreibt physikalische Phänomene, wie sie in *Inertialsystemen* beobachtet werden. Das sind unbeschleunigte Bezugssysteme. Alle solchen Systeme haben relativ zueinander konstante Geschwindigkeiten (solange keine Gravitation ins Spiel kommt, und *die* wird von der speziellen Relativitätstheorie *nicht* beschrieben). In gewisser Weise kann man sagen, dass eine wesentliche Aussage der speziellen Relativitätstheorie die *Existenz* solcher Inertialsysteme ist.

Will man die physikalische Gesetzmäßigkeiten, die ein beschleunigter Beobachter feststellt, aus der speziellen Relativitätstheorie ableiten, so ist immer Vorsicht angebracht. Das Unterfangen ist nicht unmöglich, denn letztlich ist die *allgemeine Relativitätstheorie* (mit einigen Zusatzannahmen) so gefunden worden. 

Next: Unsichtbarkeit Lorentz-Kontraktion   Up: Spezielle Relativitätstheorie   Previous: Zeitdilatation

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO