4. Kausalität

Next: Attentat auf Rhodan    Up: Kurs   Previous: Auflösung Bellsches Paradoxon

Obwohl in der Physik Kausalität oft direkt mit der zeitlichen Reihenfolge von Ereignissen verknüpft wird, ist es nicht opportun, eine *Definition* von Kausalität auf diese Reihenfolge zu stützen. Denn man kann sich ja durchaus Zeitreisen *vorstellen*, die *nicht* mit einem Paradoxon verknüpft zu sein scheinen. Macht man den Kausalitätsbegriff an der zeitlichen Reihenfolge fest, hat man mit *jeder* Zeitreise eine Verletzung der Kausalität, kann also kaum Aussagen über Möglichkeit oder Unmöglichkeit aus einer Verletzung des Kausalitätsprinzips ableiten. (Die Unmöglichkeit wäre bloß postuliert, nicht erwiesen.)

Deshalb benütze ich hier eine Definition von Kausalität, die die zeitliche Reihenfolge von Ereignissen offenlässt. Wir sagen, dass zwischen zwei Ereignissen A und B (wobei Ereignisse jetzt zeitlich lokalisierte Vorgänge sind) ein Kausalzusammenhang besteht, wenn die Verhinderung eines der Ereignisse, nehmen wir an, dies sei A, zur Folge hat, dass auch das andere, in unserem Fall also B, nicht stattfindet. Wir nennen dann A (eine) *Ursache* von B. (B kann natürlich auch mehrere Ursachen haben.) Als *Kausalprinzip* bezeichnen wir dann die Asymmetrie der Beziehung zwischen A und B: wenn A Ursache von B ist, kann B nicht Ursache von A sein. Die Verhinderung von B würde auf A keinen Einfluss haben. B nennt man *Wirkung*.

Mathematisch gesehen, erzeugt die Kausalität auf der Menge der Ereignisse eine sogenannte *Halbordnung*. Ereignisse *müssen* nicht in kausalem Zusammenhang stehen, aber *wenn* sie es tun, kann man sie aufgrund des Zusammenhangs in eine Reihenfolge bringen, indem man immer die Ursache vor der Wirkung anordnet (üblicherweise stimmt diese Reihenfolge mit der zeitlichen Reihenfolge überein). Eine solche Folge von Ereignissen würde man *Kausalkette* nennen. Offensichtlich ist in einer Kausalkette (A B C ... X) das Ereignis A Ursache aller folgenden Ereignisse, B Ursache aller Ereignisse außer A, usw..

Das hier beschriebene Kausalprinzip stimmt mit unserer Alltagserfahrung überein (man wird sich schwer tun, Beispiele von Ursache-Wirkung-Beziehungen zu finden, wo die Wirkung die Ursache verändert) und ist deshalb plausibel. Es gilt auch in der Quantenmechanik noch, weil es hinreichend schwach formuliert ist. Die in der Quantenmechanik auftretende Kausalitätsverletzung hat mit einem stärkeren Kausalprinzip zu tun, das etwa behaupten würde, dass jedes Ereignis auch tatsächlich Ursachen hat, die es vollständig bestimmen (was in der Quantenmechanik nicht gilt).

Wenn nun das Kausalprinzip gilt, so sind sogenannte *kausale Schleifen* unmöglich. Eine kausale Schleife ist eine Kausalkette, die dasselbe Ereignis X zweimal enthält. Sie wäre also von der Form (A B ...X ...U V W ... X). Damit aber ist X gleichzeitig Ursache der Ereignisse U V W und wird von ihnen verursacht, was dem Kausalprinzip widerspricht. Ebenso unmöglich sind kausale Schleifen der "zweiten Art", in denen sowohl X als auch ^X ("nicht X") auftreten (die logische Struktur würde uns hier nicht zwingen, von Schleifen zu reden, da X und ^X nicht identische Ereignisse sind; aber der Raumzeitpunkt, der X bzw. ^X zuzuordnen ist, ist derselbe, deshalb ist der Begriff Schleife auch hier sinnvoll).

Die üblichen Zeitparadoxa vom Typ "Mensch reist in die Vergangenheit und tötet seinen Vater" entsprechen kausalen Schleifen der zweiten Art.

Eine kausale Schleife der ersten Art wäre etwa bei der "Erschaffung von Gegenständen durch Zeitreise" gegeben. Beispiel: ein Zeitreisender besucht seinen Urahn und übergibt ihm die Pläne für die Zeitmaschine, woraufhin der sie baut. Hier ist das Ereignis X, die Zeitreise, sowohl Ursache als auch Wirkung des Ereignisses Y, Bau der ersten Zeitmaschine. Auf den ersten Blick hat man hier keinen Widerspruch, kein Paradox. Aber natürlich ist das Kausalprinzip verletzt. Und man kann offensichtlich die Frage nicht beantworten, woher denn nun wohl die Pläne der Zeitmaschine eigentlich kamen. Dass das ganze problematisch ist, sieht man, wenn man sich vorstellt, dass die zurückgeschickten Pläne identisch mit denen sind, die zum Erstbau verwendet wurden. Wie steht es dann mit dem Alter des Papiers? Da die Pläne von ihrer Benützung zum Bau der Maschine bis zum Zurückschicken in die Vergangenheit jedesmal um die gleiche Zeitspanne altern, muss das Papier unendlich alt sein... (es sei denn, es würde bei der Rückkehr in die Vergangenheit wieder "jünger", was aber andere Probleme hervorriefe).

Gilt also das Kausalprinzip, sind kausale Schleifen in Strenge unmöglich. Das ist eine Konsequenz der Logik und hat nichts mit speziellen physikalischen Gesetzen zu tun. Umgekehrt: sollte es doch kausale Schleifen geben, so kann das Kausalprinzip nicht gelten. (Interessanterweise lässt die *allgemeine* Relativitätstheorie Lösungen für die Metrik der Raumzeit zu, in denen kausale Schleifen möglich sind. Will man diese Lösungen ausschließen, muss man also über die Grundgleichungen der allgemeinen Relativitätstheorie hinausgehende Forderungen an die Lösung stellen.)

Eine Möglichkeit, Zeitreisen zu erlauben, aber kausale Schleifen auszuschließen, bestünde etwa darin, anzunehmen, dass die Zeit mehrdimensional ist. Zweidimensional genügt schon. Man würde sich dann nach einer Zeitreise in die Vergangenheit auf einem "Parallelstrang" zum üblichen Zeitstrom bewegen, auf dem man völlige Handlungsfreiheit hätte. Die eigene ursprüngliche Gegenwart bliebe unbeeinflusst. Manche Geschehnisse in der Perry-Rhodan-Serie, die ansonsten rätselhaft blieben, lassen sich so noch mit Sinn erfüllen, etwa die Vorstellung, dass ein Objekt, das sich "dauerhaft" 5 Minuten in der Zukunft befinde, nicht zugänglich sei (bei einer eindimensionalen Zeit würde es einfach nach 5 Minuten wieder auftauchen, ob dauerhaft 5 Minuten in der Zukunft oder nicht). Oder auch die "Beseitigung" der PAD-Seuche per Zeitparadox. (Man muss sich allerdings klarmachen, dass der Perry Rhodan der ersten Handlungsebene nichts davon hatte. Die PAD-Seuche wurde nur auf dem Parallelstrang beseitigt, die erste Handlungsebene muss als verloren angesehen werden. Wenigstens, solange man auf Logik besteht...)

Wie steht es nun mit der Kausalität in der speziellen Relativitätstheorie, in der die Zeit eindimensional vorausgesetzt wird? Wir haben schon gesehen, dass unsere mit Tachyonenpistolen ausgerüsteten Duellanten das Kausalprinzip verletzen würden. (Allerdings liegt in diesem Beispiel keine einfache Kausalschleife vor, eher eine Wechselwirkung zweier sich gegenseitig ausschließender Schleifen. Man könnte eine einfache Schleife erzeugen, indem man annimmt, dass einer der beiden Duellanten, z.B. Alf, zu betrügen versucht, indem er *vor* Sekunde 6 schießt. Er trifft dann Bert bei dessen Sekunde 3.6 in den Rücken. Aber Bert, empört über den Betrug, schafft es noch, sich herumzuwerfen und zurückzuschießen. Er trifft Alf tödlich, bei dessen Sekunde 2.16 und verhindert damit, dass Alf schießen kann. Dann aber wird er nicht bei Sekunde 3.6 getroffen, schießt also nicht eher als vorgesehen, also überlebt Alf bis Sekunde 6, also kann Alf schießen, usw.)

Zu zeigen bleibt, dass ohne überlichtschnelle Signale eine Kausalstruktur möglich ist und wie diese aussieht.

Im Fall der Newtonschen Mechanik ist die Kausalstruktur extrem einfach: solange zwei Ereignisse nicht gleichzeitig sind, können sie in einem Kausalzusammenhang stehen und das frühere Ereignis muss dann die Ursache sein, das spätere die Wirkung (Zeitreisen wären auch bei Newton problematisch).

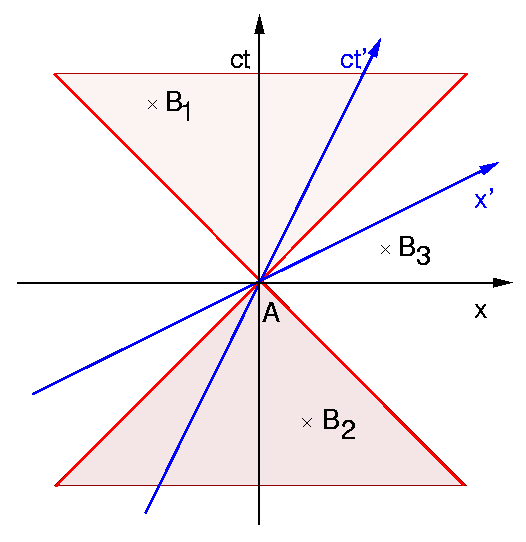
In der Relativitätstheorie ist ein kausaler Zusammenhang zwischen zwei Ereignissen nur dann möglich, wenn ihre zeitliche Reihenfolge *beobachterunabhängig* ist. Das bedeutet, dass, wenn man eines der Ereignisse in den Koordinatenursprung setzt, sich das andere im Vorwärts- oder Rückwärtslichtkegel befinden muss. Das ist im ersten Bild dargestellt. A ist unser zu untersuchendes Ereignis. B_1 befindet sich im Vorwärtslichtkegel, B_2 im Rückwärtslichtkegel von A. B_1 könnte eine Wirkung von A sein, B_2 eine Ursache. Da der bei (x,t)=(0,0) zentrierte Lichtkegel für einen beliebigen relativ zu A bewegten Beobachter derselbe ist, sind sich alle Beobachter darüber einig, dass die Möglichkeit eines kausalen Zusammenhangs zwischen A und B_1 bzw. B_2 besteht, ebenso darüber, dass B_1 nur Wirkung, B_2 nur Ursache von A sein kann. Man sagt in diesem Fall, dass A und B_1 bzw. A und B_2 *zeitartig* zueinander liegen. Ein Ereignis, das *auf* dem Lichtkegel von A liegt (auf den roten Linien), kann auch noch in kausalem Zusammenhang mit A stehen. In diesem Grenzfall spricht man von *lichtartiger* Lage der beiden Ereignisse. Das Ereignis B_3 hingegen liegt außerhalb des Lichtkegels von A. Eine solche Lage bezeichnet man als *raumartig*. Ereignis B_3 könnte von A nur beeinflusst werden, wenn es überlichtschnelle Signale gäbe. In dem Fall wäre aber für den blauen Beobachter die *zeitliche* Reihenfolge entgegengesetzt zur Ursache-Wirkungs-Folge. Man kann dann durch geeignete Wahl einer Folge von Bezugssystemen eine raumartige Schleife aus jeweils zukunftsgerichteten Bahnen konstruieren -- ein Problem für die Kausalität.

Die Schlussfolgerung ist, dass Objekte und Signale sich eben nur auf zeitartigen, bestenfalls lichtartigen Bahnen bewegen können (d.h. Bahnen, bei denen zwei infinitesimal voneinander entfernte Punkte zeitartig bzw. lichtartig zueinander liegen).

Das heißt nicht, dass es "nichts" gäbe, was sich schneller als das Licht bewegt. Schatten zum Beispiel können sehr leicht schneller als das Licht sein. Das demonstriert das Bild rechts. Das große gelbe Etwas am oberen Bildrand soll der Mond sein. Auf der Erde haben wir eine kleine schwarze Kugel (kaum sichtbar) und einen Laser, der diese schönen magentafarbenen Strahlen aussendet, so dass der Schatten der Kugel auf den Mond fällt (oben links und oben rechts). Dann wird der Laser schnell um einen kleinen Winkel um das Zentrum der Kugel gedreht, so dass der Schatten vom linken Mondrand zum rechten wandert. Wie schnell können wir ihn kriegen? Nehmen wir an, dass der Laser 1 m von der Kugel entfernt ist. Der Winkeldurchmesser des Mondes von der Erde aus gesehen ist 30 Bogenminuten; wenn wir also den Schatten über den ganzen Mond wandern lassen wollen, müssen wir den Laser um 30' drehen. Die Strecke, um die er dabei wandert, beträgt 100 cm * 6.28 *30/(60*360) = 0.87 cm. Wenn wir die Drehung in einer Tausendstel Sekunde bewerkstelligen wollen, müssen wir dem Laser also eine Geschwindigkeit von 8.7 m/s = 31.4 km/h verleihen, was vielleicht nicht einfach ist, aber durchaus machbar. In derselben Zeit (wenn auch um etwa eine Sekunde versetzt), bewegt sich der Schatten auf dem Mond über dessen Durchmesser, also rund 3400 km. Das macht eine Geschwindigkeit von 3400 km * 1000/s = 3.4 Millionen km/s, etwa 10fache Lichtgeschwindigkeit. Natürlich braucht das Licht des Lasers von der Erde zum Mond mehr als eine ganze Sekunde (die Entfernung ist im Mittel 384 000 km), aber die braucht es für *beide* Extrempositionen des Schattens, der also tatsächlich in einer 1000stel Sekunde über den ganzen Mond wandert. Und natürlich kann man das nicht zum Transport von Nachrichten *zwischen* den beiden Schattenpositionen verwenden. Man kann es allerdings zum Synchronisieren ausnützen. Nehmen wir an, die Amerikaner hätten zwei Mondstationen oben und wollten Ihren Nationalfeiertag mit (vakuumtauglichem) Feuerwerk in beiden simultan begehen. Dann könnte man das von der Erde aus mit einem solchen Laser bewerkstelligen. Dass keine Nachrichtenübertragung auf dem Mond stattfindet, sieht man leicht, wenn man sich vorstellt, dass die "bösen" Russen das harmlose Vergnügen der Amerikaner stören wollen und den linken Schatten mit einem gleichartigen Laser ableuchten. Dann kommt der rechte immer noch an, und die Feuerwerksraketen gehen nur an einer Stelle hoch, denn es gibt keine Möglichkeit für die Bewohner der linken Station, die der rechten rechtzeitig zu informieren, dass sie keinen Schatten gesehen haben.

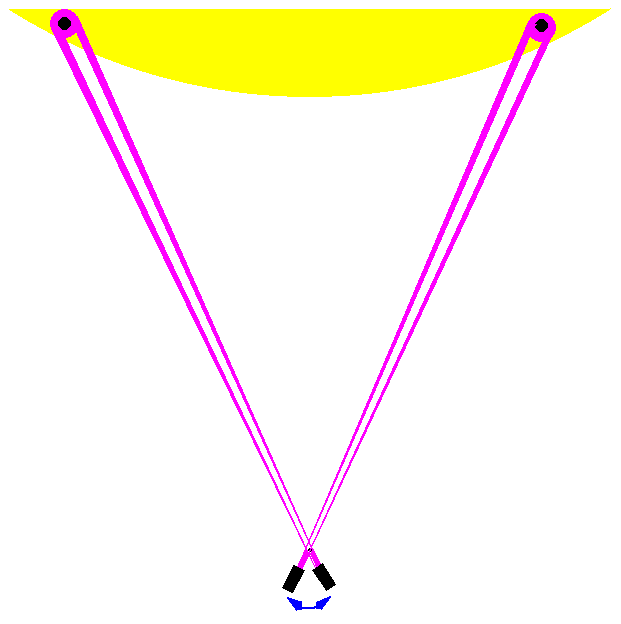Statt Schatten kann man natürlich auch einfach den Lichtfleck nehmen, den der Laser macht. Der wandert auch überlichtschnell über den Mond. Was hier passiert, ist einfach, dass wir mental Entitäten zu einem "Objekt" zusammenfassen, die tatsächlich keine Objekte sind.

Natürlich ist jeder einzelne Schatten oder Lichtfleck objektiv da, also durchaus ein Objekt. Aber die verschiedenen Schatten an verschiedenen Orten auf dem Mond sind eigentlich nicht *dasselbe* Objekt sondern *verschiedene* Objekte, die kausal nicht miteinander zusammenhängen, obwohl sie natürlich dieselbe Ursache haben (den Laser auf der Erde). (Kausaler Zusammenhang ist hier in dem oben erklärten Sinn gemeint.)

Ein vielleicht noch verblüffenderes Beispiel: Es ist möglich, ein Tuch mit einer geeigneten Schere *überlichtschnell durchzuschneiden*. Dabei wandert der Schnittpunkt der beiden Schneiden mit Überlichtgeschwindigkeit durch das Tuch. Allerdings sollte man dazu keine Schere nehmen, die auf der Hebelwirkung um einen Angelpunkt beruht. Denn die Wirkung, die von diesem Punkt ausgeht, kann sich nicht schneller als das Licht zur Spitze der Schere fortpflanzen, was bedeutet, dass diese in der Nähe des Angelpunktes schon zu schneiden beginnt, bevor die Spitze sich überhaupt bewegt. Die Schneide muss sich in diesem Fall also biegen. Besser ist es, die Schere aus zwei nichtzusammenhängenden Scherblättern zu machen, die von synchronisiert gezündeten Raketen angetrieben werden, so dass sich die gesamte Schneide zu einem Zeitpunkt beginnt, parallel zu verschieben. Wenn man den Winkel a zwischen den Scherblättern klein genug macht, kann man offenbar jede Schnittgeschwindigkeit erreichen, denn der Schnittpunkt bewegt sich mit der Geschwindigkeit v/sin a, wenn eines der Scherblätter ruht und das andere sich senkrecht zu seiner eigenen Richtung mit Geschwindigkeit v (< c) bewegt (parallelverschiebt). Der Fall a = 0 ist besonders transparent: dann sind die Scherblätter parallel und die Schnittgeschwindigkeit ist exakt unendlich, da alle Teile des Tuches entlang der Schnittlinie zum selben Zeitpunkt durchtrennt werden. (Natürlich ist für einen anders bewegten Beobachter die Schnittgeschwindigkeit nicht unendlich, da er eine andere Gleichzeitigkeit hat. Woraus man folgern kann, dass für ihn die Scherblätter nicht parallel sind... Überlichtschnell ist diese Geschwindigkeit aber für jeden Beobachter.) Man erkennt wieder, dass das Durchschneiden des Tuches an einem Ort nichts mit dem an einem anderen zu tun hat, dass kein kausaler Zusammenhang zwischen diesen Ereignissen existiert.

Ähnliche Erklärungen gibt es für eine Vielzahl möglicher überlichtschneller Bewegungen, denen allen gemeinsam ist, dass keine Energie und keine Information transportiert werden. Das gilt zum Beispiel auch (trotz teilweise anderslautender Behauptungen) für das Quantentunneln, das als Mittel des überlichtschnellen Transports durch die Presse ging und sehr leicht mit vergleichbaren Überlegungen verstanden werden kann.

*Nicht leicht* zu verstehen sind hingegen die Quantenkorrelationen, die mit der Verletzung der *Bellschen Ungleichungen* verknüpft sind und Möglichkeiten wie das "Teleportieren" eines Quantenspins implizieren. Ich glaube, dass dies bisher niemand wirklich versteht. Obwohl man es natürlich berechnen kann.

Doch nun zurück zur Relativitätstheorie und ihren Auswirkungen auf ein Universum, in dem überlichtschnelles Reisen möglich sein soll. Das bringt mich zur bereits erwähnten Perry-Rhodan-Geschichte.

Next: Attentat auf Rhodan    Up: Kurs   Previous: Auflösung Bellsches Paradoxon

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO