6. Die Lorentzsche Äthertheorie

Up: Kurs   Previous:Attentat auf Rhodan

Dieser letzte Teil des Kurses befasst sich mit einer Möglichkeit, die spezielle Relativitätstheorie umzuinterpretieren. Von *Interpretation* sollte man dabei allerdings nur insoweit sprechen, als dieser Ansatz bei Unterlichtgeschwindigkeiten zu denselben Vorhersagen für experimentelle Ergebnisse führt wie die SRT. Für überlichtschnelle Bewegungen, wenn man sie denn als möglich annimmt, weichen seine Vorhersagen von denen der SRT ab. Man muss diese Struktur dann schon als eine eigene *Theorie* betrachten, nicht bloß als eine neue Interpretation einer bereits vorhandenen Theorie.

Als Einstein seine spezielle Relativitätstheorie veröffentlichte, waren verschiedene der von dieser vorhergesagten Effekte schon bekannt. Wenn man bedenkt, wieviel seine Vorgänger Lorentz und Poincaré zu der Zeit schon wussten, kann man sich durchaus fragen, warum nicht einer von ihnen die SRT entwickelt hat.

Bekannt waren die Lorentzkontraktion und die Zeitdilatation; aus ihnen wurde aber *nicht* die Folgerung einer nichtobjektiven Gleichzeitigkeit gezogen. Stattdessen hatte Lorentz die Vorstellung, dass ein *relativ zum Äther* bewegter Körper kontrahiert und dass eine von ihm mitgeführte Uhr langsamer geht, als in einem System das relativ zum Äther ruht. Diese Effekte sollten das Ergebnis einer wie auch immer gearteten Wechselwirkung bewegter Objekte mit dem Äther sein.

Hier gibt es also keine echte Symmetrie zwischen den Inertialsystemen. Die Zeit des Beobachters im (auf den Äther bezogen) bewegten System läuft "wirklich" langsamer als die des ruhenden, während die Tatsache, dass der bewegte Beobachter die Zeit des ruhenden langsamer laufen "sieht", eine Täuschung ist, die auf den (eher zufälligen) Symmetrieeigenschaften der Lorentztransformation beruht. Der *bewegte* Körper ist "wirklich" kürzer, die Verkürzung eines *ruhenden* Körpers aus der Sicht des bewegten ist eine Täuschung, beruhend auf dem Zusammenwirken der Kontraktion bewegter Maßstäbe und des Langsamerlaufens bewegter Uhren. ("Bewegt" und "ruhend" haben jetzt natürlich absolute Bedeutung. Sie werden immer auf den Äther bezogen, der ein für alle verbindliches Ruhsystem festlegt.)

Man kann Einsteins und Lorentzens Vorstellungen etwa so charakterisieren: Bei Einstein sind Längenkontraktion und Zeitdilatation Konsequenzen der Struktur der Raumzeit selbst (ein bewegter Maßstab verändert sich selbst überhaupt nicht, aber die relativen Gewichte von Raum und Zeit sind für verschieden bewegte Maßstäbe verschieden, nicht die Uhr ändert sich bei einer Bewegung, sondern die Zeit selbst), bei Lorentz sind sie Wirkungen auf die Materialien, (d.h. bewegte Maßstäbe verkürzen sich, bewegte Uhren gehen langsamer) so dass Zeit und Raum verändert *erscheinen*, obwohl sie es nicht wirklich sind. Lorentz lässt also Zeit und Raum fest und verändert die Eigenschaften der Materialien, während Einstein die Eigenschaften der Materialien unverändert lässt und Zeit und Raum ändert (wobei die *Raumzeit* ungeändert bleibt).

Solange die beiden Theorien dieselben Voraussagen machen, kann man trefflich darüber streiten, ob sie sich inhaltlich überhaupt unterscheiden. Der Streit ist vergleichbar dem, ob es sich um unterschiedliche Situationen handelt, wenn alle Maßstäbe sich verkleinern oder wenn sie fest bleiben und der Raum sich vergrößert. Solange *alle* Maßstäbe betroffen sind, ist *operational* eine Unterscheidung nicht möglich, so dass man meinen mag, die beiden Situationen seien identisch.

Nichtsdestotrotz gibt es offenbar eine ganze Menge Leute, die sich tatsächlich was Unterschiedliches darunter vorstellen können, so dass man der Diskussion nicht gut ausweichen kann. (Es genügt ja, wenn *ein* Maßstab vom allgemeinen Verhalten abweicht, um eine Entscheidung zu treffen.) Ähnlich ist es mit der Frage, ob die scheinbare Kontraktion im Ruhsystem des Äthers und die wahre Kontraktion in einem bewegten System wirklich unterschiedliche Dinge sind.

Mit der Kantschen Philosophie scheint auf den ersten Blick nur die Lorentzsche Äthertheorie vereinbar, denn nur in ihr können Raum und Zeit als a priori Anschauungsformen, die nicht als *Objekte* wissenschaftlichen Denkens weiter analysierbar sind, angenommen werden. Durch geeignete Uminterpretation dessen, was wirklich a priori ist und dessen, was Gegenstand wissenschaftlicher Empirie sein kann, lässt sich Kant wohl letztlich auch mit der Gedankenwelt der speziellen Relativitätstheorie in Einklang bringen. Außerdem gibt es da noch die Philosophie der evolutionären Erkenntnistheorie, die versucht, die Kantschen a prioris als a posterioris innerhalb der Entwicklung der Spezies zu erklären. D.h., es gibt noch eine tiefere Ebene als die der Kantschen Anschauungsformen. Nichtsdestotrotz passen die Kantschen Vorstellungen sehr viel besser mit der Lorentzschen Äthertheorie zusammen als mit der Relativitätstheorie. Denn in der ersteren sind Raum und Zeit wirklich nicht an der Physik teilnehmende Objekte, sondern nur der notwendige (= a priori) Hintergrund für die Beschreibung einer Dynamik, die durch die Wechselwirkung mit dem Äther geprägt ist.

Peter Holzer hat in einem seiner Postings gesagt, dass er die spezielle Relativitätstheorie wegen ihrer größeren Einfachheit vorziehe. Nun ist Einfachheit bis zu einem gewissen Grad Geschmackssache. In einem formalen Sinn ist die Relativitätstheorie einfacher, weil sie ein Konzept weniger benötigt -- es tritt kein Äther auf. Andererseits scheint sie dies nur zu erreichen, indem sie Raum und Zeit komplexer macht, die ja in der Äthertheorie richtig schön trivial sind.

Meine ursprüngliche Einstellung hierzu war, dass die Lorentzsche Äthertheorie weniger *erklärt*. Denn in der speziellen Relativitätstheorie ist die Reziprozität der Zeitdilatation und der Längenkontraktion eine Folge einer zugrundeliegenden Symmetrie der Raumzeit. In der Lorentzschen Äthertheorie bleibt sie unerklärt. Es ist absolut nicht einzusehen, warum sich die physikalischen Gesetze derart verschwören sollten, dass es unmöglich wird, den an ihrem Zustandekommen wesentlich mitwirkenden Äther zu detektieren.

Inzwischen bin ich mir diesbezüglich nicht mehr so sicher. In dem Buch von Helmut Günther: Grenzgeschwindigkeiten und ihre Paradoxa (Teubner, Stuttgart, Leipzig, 1996) wird ein festkörperphysikalisches Modell der Relativitätstheorie aufgestellt. In diesem Modell treten die Lorentztransformationen mit der Schallgeschwindigkeit als Grenzgeschwindigkeit als die relevanten Transformationen bei einer Beschreibung der Dynamik von Versetzungen in einer Kontinuumsnäherung auf. Der Äther ist hier der Festkörper, der natürlich eine Gitterstruktur hat. Die speziellen Eigenschaften der Lorentztransformationen sind Folge des Übergangs vom Gitter zum Kontinuum [1]. Das heißt, man hat hier ein Modell, in dem das Verschwinden jeglicher Referenz auf den Bewegungszustand des zugrundeliegenden Festkörpers sich auf natürlich Weise im Rahmen eines Kontinuumsübergangs erklärt. Man kann das als eine Erweiterung der Lorentzschen Äthertheorie sehen und würde dann vermuten, dass der Äther, den wir zur Erzeugung der Lorentztransformationen in der speziellen Relativitätstheorie brauchen, auch eine Gitterstruktur hat. Die Lorentzinvarianz wäre dann nur auf Längenskalen gültig, die groß gegen die Gitterkonstante sind. Auf kleineren Skalen sollte die Gitterstruktur sich bemerkbar machen.

Allerdings ist im Auge zu behalten, dass das Modell nur zweidimensional ist und sich anscheinend nicht in einfacher Weise auf eine vierdimensionale Raumzeit erweitern lässt. In einem dreidimensionalen Festkörper gibt es immer mindestens zwei verschiedene Schallgeschwindigkeiten, eine für Longitudinalwellen und eine für Transversalwellen, und die Lorentztransformationen lassen natürlich nur *eine* Grenzgeschwindigkeit zu. Außerdem wird in dem Modell die Annahme gemacht, dass Längen- und Zeitmaßstäbe durch die Kink- bzw. oszillatorischen Lösungen einer nichtlinearen Gleichung für die Kontinuumsdynamik von Versetzungen gegeben sind (der Sine-Gordon-Gleichung). Diese Gleichung ist aufgrund des Kontinuumslimes lorentzinvariant, und das impliziert dann natürlich die Effekte der speziellen Relativitätstheorie für die solchermaßen definierten Längen und Zeiten. Die Überzeugungskraft des Arguments von Günther, dass es *natürlich* sei, die Längen- und Zeitmaßstäbe so festzulegen, beruht wesentlich auf der Beschränkung auf die Versetzungsdynamik, in der eben das Kristallgitter undetektierbar wird.

Sobald es Effekte gibt, die nicht diesen Basisgleichungen genügen (z.B. die Wirkung eines Teilchens, das von außen mit Überschallgeschwindigkeit in den Kristall geschossen wird), legen sich andere Verfahrensweisen für die Definition von Längen und Zeiten nahe, und die Invarianz der "Welt" gegenüber Lorentztransformationen geht verloren.

Das aber heißt nichts anderes, als dass der Äther detektierbar und damit eine Entscheidung zwischen Relativitätstheorie und Äthertheorie zugunsten der letzteren möglich wird!

Wenn wir nun zu "unserer" Relativitätstheorie (mit der Lichtgeschwindigkeit als Grenzgeschwindigkeit) zurückgehen, so müssen wir also grundsätzlich zugeben, dass sie vorläufig von einer Äthertheorie nicht unterscheidbar ist. Das wissenschaftstheoretische Argument, das man dann noch für die spezielle Relativitätstheorie vorbringen kann, und das sie zu einer stärkeren Theorie macht als die Lorentzsche Äthertheorie, ist, dass sie bessere Möglichkeiten für ihre eigene Falsifizierung bietet als letztere. Diese Idee geht auf Popper zurück. Wenn zwei Theorien sich in ihren Aussagen hinsichtlich der gegenwärtigen experimentellen Lage nicht unterscheiden, sollte man diejenige als stärker ansehen, die schärfere Aussagen, d.i. Einschränkungen, für zukünftige Experimente macht, die also prinzipiell auf einfachere Weise falsifizierbar ist. Denn wenn sie dann nicht falsifiziert wird, hat sie offenbar schärfere Tests bestanden als die andere. Sollte man also überlichtschnelle Kommunikation etablieren, wäre damit die Relativitätstheorie falsifiziert, während die Äthertheorie weiterleben könnte. Deshalb ist, solange die SRT nicht falsifiziert ist, sie die stärkere Theorie...

Man kann allerdings die Äthertheorie hier formal auf dasselbe Niveau der Falsifizierbarkeit heben wie die spezielle Relativitätstheorie, indem man einfach postuliert, dass kein überlichtschneller Signaltransport möglich ist. In dem Fall wäre wieder "Ockham's Rasiermesser" gefragt: das zieht die Relativitätstheorie der Äthertheorie schon deshalb vor, weil sie ein Konzept weniger benötigt als diese. Wenn dann die Äthertheorie noch ein zusätzliches Postulat braucht, das innerhalb ihres Rahmens durch nichts motiviert ist, ist sie erst recht zu verwerfen.

Der einzige Reiz der Äthertheorie (abgesehen davon, dass sie es ermöglicht, mit primitiven Vorstellungen von Raum und Zeit auszukommen) ist (in meinen Augen) aber gerade, dass sie Überlichtgeschwindigkeiten ohne größere Probleme erlaubt. Diese sind dann allerdings mit einer expliziten Detektierbarkeit des Äthers verknüpft.

Sehen wir uns das am Beispiel unserer Perry-Rhodan-Geschichte an (damit dieses Elaborat doch noch ein bisschen on topic wird...). Dazu sollte man sich nochmal das Bild vom letzten Abschnitt vornehmen. 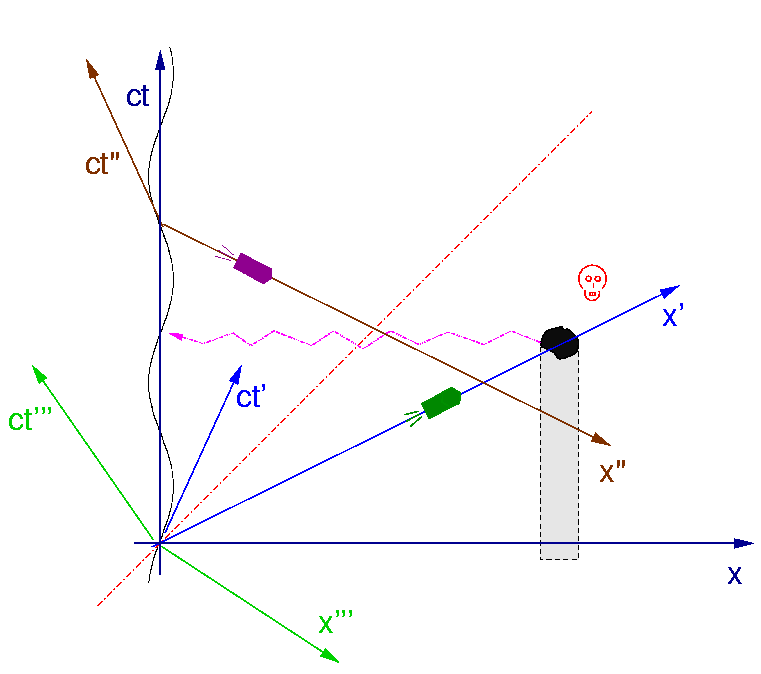Angenommen, das absolute Ruhsystem wäre identisch mit dem (x ct)-System. Das ist auch das Ruhsystem der Sonne. Dann sind sowohl Perrys Reise zum Asteroiden möglich, sie dauert in absoluter Zeit ein Jahr (obwohl sie im zum Startzeitpunkt gültigen lokalen Ruhsystem der Erde in Nullzeit stattfand), als auch die Sendung des Hilferufs zur Erde, die in absoluter Nullzeit geschieht. Atlans Rettungsaktion hingegen ist unmöglich, da sie in die absolute Vergangenheit führen würde. Das heißt, wenn es etwa im Frühling möglich war, mit praktisch unendlicher Geschwindigkeit zum Asteroiden zu fliegen, geht das im Herbst nicht mehr, es gibt eine Grenzgeschwindigkeit, die den Wert c²/v hat, wo v die Geschwindigkeit der Erde auf ihrer Bahn um die Sonne ist.

Andererseits könnte auch Atlans momentanes Ruhsystem beim Start das absolute Bezugssystem sein. In diesem Fall wäre Rhodans Reise immer noch möglich (sie würde sogar absolut länger als ein Jahr dauern), aber der Hilferuf könnte nicht geschickt werden, da er in die absolute Vergangenheit ginge. Dasselbe gilt, wenn die Sicht des Beobachters im System (x''' ct''') die absolut richtige ist. Die Rettungsaktion wäre in diesem Fall möglich und völlig undramatisch interpretierbar: Atlan ist einfach viel schneller zum Asteroiden geflogen als Perry und kommt deshalb eher dort an als dieser (kein Problem, wenn Perrys Flug länger als ein Jahr dauert -- Atlan kommt weniger als ein halbes Jahr vor Perry an). Aber natürlich konnte Atlan nichts davon wissen, dass er zur Rettung Perrys flog, denn die Nachricht war unmöglich.

Schließlich wäre es auch noch denkbar, dass das absolute System sich relativ zum Sonnensystem schneller als mit 30km/s nach rechts bewegt. In diesem Fall sind sowohl Rhodans als auch Atlans Reise unmöglich, während nichts gegen die Möglichkeit des Signals spricht.

Im Rahmen der Äthertheorie könnte also eine kausale Schleife nicht auftreten, obwohl einzelne Wegstücke der Geschichte möglich wären. Im Rahmen der speziellen Relativitätstheorie können wir keinen der Beobachter auszeichnen, es ist also nur möglich, entweder alle überlichtschnellen Wegstücke als erlaubt anzusehen oder keines. Das heißt, hier ist die kausale Schleife nicht zu vermeiden, wenn wir Überlichtgeschwindigkeit zulassen.

Wie würde man dann feststellen, welches das absolute Bezugssystem ist? Einfach, indem man die maximal erreichbare Signalgeschwindigkeit in sechs paarweise entgegengesetzten Raumrichtungen misst (von denen man drei orthogonal wählen kann). Ist sie bezüglich eines Richtungspaars c²/v in die eine und -c²/v in die Gegenrichtung (was bedeutet, dass Signale in die Vergangenheit geschickt werden können -- negative Geschwindigkeiten sind hier in einem gewissen Sinn "größer" als unendlich, weil sie durch Umdrehen der Zeit zustande kommen, nicht des Raums), so beträgt die Geschwindigkeit bezüglich des Äthers in der betrachteten Achsenrichtung v. Ist die Maximalgeschwindigkeit in beiden Richtungen unendlich, so ruht das System in dieser Achsenrichtung relativ zum Äther.

Das Perryversum sähe dann so aus, dass die lokalen Uhren auf jedem Planeten im allgemeinen mit einer Geschwindigkeit laufen würden, die von der einer Uhr im absoluten Bezugssystem verschieden wäre. Auf jedem Planeten könnte dann eine Hyperfunkstation stehen, die ein Zeitsignal von einer mit der absoluten Zeit laufenden Uhr erhielte. Würde man von einem "Ende" der Galaxis im Hyperraumflug zum anderen fliegen, also ca. hunderttausend Lichtjahre zurücklegen, so fände man, dass man sich bezüglich lokal ruhender Uhren um bis zu hunderttausend Jahre in die Zukunft oder Vergangenheit bewegt hätte. Bezüglich der absoluten Uhr wäre die Flugzeit immer positiv. Wenn der Hinflug, sagen wir, fünfzigtausend Jahre in die Zukunft ging (bzgl. einer lokalen Uhr), würde der Rückflug bei gleicher absoluter Geschwindigkeit fünfzigtausend Jahre in die Vergangenheit gehen. Man käme also nur um kurze Zeit nach dem Abflug wieder zurück (je nachdem wie lange man weg war). In der absoluten Zeit gerechnet, sähe alles so normal aus, wie heute etwa eine Flugzeugreise nach den USA und zurück, bei der man seine Uhren nicht auf die lokale Zeit umstellt.

Da das Denken in lokaler Zeit, mit Vorwärts- und Rückwärtsbewegungen, kompliziert ist, würden die Leute wahrscheinlich die absolute Zeit zur Beschreibung solcher Flüge und auch für die Geschichtsschreibung verwenden. Möglicherweise würde man sogar für die allgemeine Zeitmessung die Absolutuhr verwenden. Bei Systemen mit sehr hoher Relativgeschwindigkeit bezüglich des Absolutsystems hätte das allerdings den Nachteil einer starken Abweichung des Zeitgefühls von der angegebenen Uhrzeit. Und natürlich gibt es keinen Grund anzunehmen, dass etwa unsere Milchstraße sich nicht sehr schnell bezüglich des Absolutsystems bewegt. Wenn sie sich mit etwa mit 99% der Lichtgeschwindigkeit relativ zu diesem bewegt, würde die Absolutzeit um ca. einen Faktor 7 schneller gehen als die auf lokalen Uhren gemessene, d.h., auf der aufgestellte Absolutuhr vergingen pro Tag 168 Stunden, also eine ganze Woche... Innerhalb der Milchstraße wäre dieser Faktor allerdings praktisch überall der gleiche (außer natürlich in Raumschiffen), so dass das für das tägliche Leben kein großes Problem entstünde. Erst wenn man intergalaktisch über Distanzen von tausend Megaparsek o.ä. verkehrt, würden diese Dilatationsfaktoren wegen ihrer Verschiedenheit in weit voneinander entfernten Galaxien relevant (diese Galaxien haben ja große Relativgeschwindigkeiten). Allerdings müsste man dann die Betrachtungen ohnehin auf die allgemeine Relativitätstheorie ausdehnen und für die eine substituierende Äthertheorie finden. (Denn über solche Entfernungen wird die globale Krümmung der Raumzeit wichtig.) Und das Problem würde nochmal, eventuell stark, modifiziert...

[1] Hier muss ich mich korrigieren. Mittlerweile (2001) habe ich verstanden, dass das Auftreten von Lorentz-Invarianz nicht Konsequenz des Übergangs vom Gitter zum Kontinuum ist. Wenn man diesen Übergang exakt durchführt, bleibt das System galilei-invariant und man erhält auch nicht die übliche Wellengleichung. Diese entsteht erst durch eine Vernachlässigung, bei der der advektive Term einer substantiellen Zeitableitung weggelassen wird und diese durch eine partielle Zeitableitung ersetzt wird. Dies entspricht dem Übergang von einer Lagrangeschen zu einer Eulerschen Betrachtungsweise, hier allerdings über eine Näherung. Das Auftreten der Lorentz-Invarianz anstelle der Galilei-Invarianz ist also Konsequenz dieser Näherung und nicht des Kontinuumslimes.

Damit kehre ich sozusagen gefestigt zu meiner alten Einstellung zurück, dass die Lorentzsche Äthertheorie an einem Erklärungsdefizit leidet.

Up: Kurs   Previous: Attentat auf Rhodan